字符串的朴素匹配与KMP模式匹配

视频讲解，习题讲解，思维导图，PPT资源

链接: https://pan.baidu.com/s/15c5BVuCkY1lSOmIoDM1XxA 密码: v4pc

1. 串的基本定义

串，即字符串(String)是由零个或多个字符组成的有限序列。一般记为 S = ‘a₁ a₂······a_n‘ (n≥0)

其中，S是串名，单引号括起来的字符序列是串的值；a_i可以是字母、数字或其他字符；串中字符的个数n称为串的长度。n= 0时的串称为空串(用∅表示)。

例:

有的地方用双引号(如Java、C)，有的地方用单引号(如python)

S=”HelloWorld!”

T=”iPhone 11 Pro Max?”

子串：串中任意个连续的字符组成的子序列。 Eg：’iPhone’，’Pro M’ 是串T 的子串

主串：包含子串的串。 Eg：T 是子串’iPhone’的主串

字符在主串中的位置：字符在串中的序号。 Eg：‘1’在T中的位置是8(第一次出现)

子串在主串中的位置：子串的第一个字符在主串中的位置。Eg：’11 Pro’在 T 中的位置为8

空串 V.S 空格串:

M=‘’“ 是空串

N=‘ ’ 是由三个空格字符组成的空格串，每个空格字符占1B

串是一种特殊的线性表，数据元素之间呈线性关系

串的数据对象限定为字符集(如中文字符、英文字符、数字字符、标点字符等)

串的基本操作，如增删改查等通常以子串为操作对象

2. 串的基本操作

假设有串T=“”，S=”iPhone 11 Pro Max?”，W=“Pro”

StrAssign(&T,chars)：赋值操作。把串T赋值为chars。

StrCopy(&T,S)：复制操作。由串S复制得到串T。

StrEmpty(S)：判空操作。若S为空串，则返回TRUE，否则返回FALSE。

StrLength(S)：求串长。返回串S的元素个数。

ClearString(&S)：清空操作。将S清为空串。

DestroyString(&S)：销毁串。将串S销毁(回收存储空间)。

Concat(&T,S1,S2)：串联接。用T返回由S1和S2联接而成的新串

SubString(&Sub,S,pos,len)：求子串。用Sub返回串S的第pos个字符起长度为len的子串。

Index(S,T)：定位操作。若主串S中存在与串T值相同的子串，则返回它在主串S中第一次出现的位置;否则函数值为0。

StrCompare(S,T)：比较操作。若S>T，则返回值>0；若S=T，则返回值=0;若S<T，则返回值<0。

“abandon” < “aboard” ：从第一个字符开始往后依次对比，先出现更大字符的串就更大
“abstract” < “abstraction”：长串的前缀与短串相同时，长串更大
“academic”=“academic”：只有两个串完全相同时，才相等

Eg：

执行基本操作 Concat(&T, S, W) 后，T=“iPhone 11 Pro Max?Pro” – 存储空间扩展?

执行基本操作 SubString(&T ,S, 4, 6)后，T=“one 11”

执行基本操作 Index(S, W)后，返回值为 11

3. 字符集编码

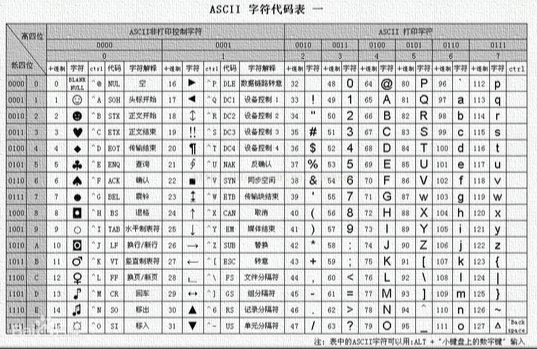
任何数据存到计算机中一定是二进制数。

需要确定一个字符和二进制数的对应规则，这就是“编码”

对应y = f(x) —— 字符集：函数定义域 —— 编码：函数映射规则f —— y：对应的二进制数

“字符集”：英文字符—ASCII字符集，中英文—Unicode字符集

基于同一个字符集，可以有多种编码方案，如：UTF-8，UTF-16

注：采用不同的编码方式，每个字符所占空间不同，考研中只需默认每个字符占1B即可

乱码问题

在你的文件中，原本采用某一套编码规则y=f(x)，如 : ‘码’↔0001010100010101010010

打开文件时，你的软件以为你采用的是另一套编码规则y=g(x)，如: 0001010100010101010010

4. 串的存储结构

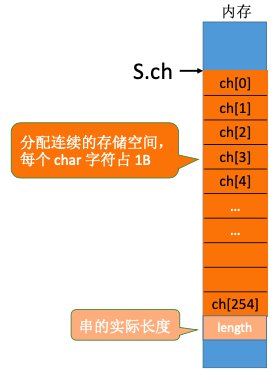
4.1. 顺序存储

4.1.1. 静态数组-定长顺序存储

//预定义最大串长
#define MAXLEN 255
typedef struct{
  //每个分量存储一个字符-定长顺序存储
  char ch[MAXLEN];
  //串的实际长度
  intlength;
}SString;

4.1.2. 动态数组-堆分配存储

在C语言中，存在一个称之为“堆”的自由存储区，并用malloc()和free()函数来完成动态存储管理。

typedef struct{
  //按串长分配存储区，ch指向串的基地址
  char *ch;
  int length;
}HString;

HString S;
S.ch=(char*)malloc(MAXLEN*sizeof(char));
S.length=0;

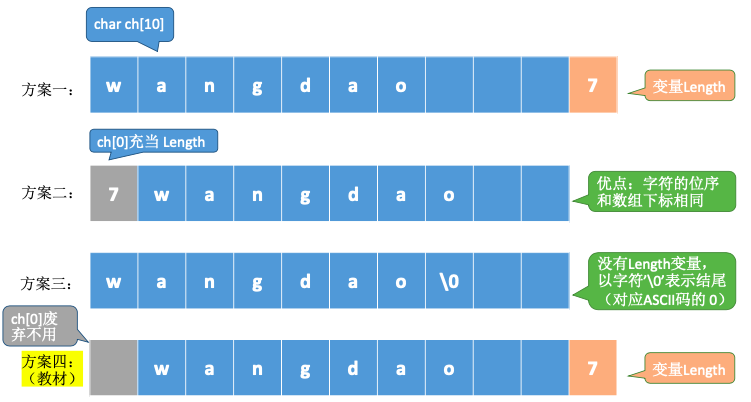
4.1.3. 如何记录串长length

4.2. 链式存储

存储密度低，每个字符1B，每个指针4B

typedef struct StringNode{
  //每个结点存1个字符
  char ch;
  struct StringNode *next;
}StringNode,*String;

提高存储密度

typedef struct StringNode{
  //每个结点存1个字符
  char ch[4];
  struct StringNode *next;
}StringNode,*String;

4.3. 基于顺序存储实现基本操作

#define MAXLEN 255
typedef struct{
  char ch[MAXLEN];
  intlength;
}SString;

4.3.1. SubString(&Sub,S,pos,len)

求子串。用Sub返回串S的第pos个字符起长度为len的子串。

S.ch=”wangdao” S.length=7

bool SubString(SString &Sub,SString S,int pos,int len){
  //子串范围越界
  if(pos+len-1>S.length){
    return false;
  }
  for(int i=pos;i<pos+len;i++){
    Sub.ch[i-pos+1]=S.ch[i];
  }
  Sub.length=len;
  return true;
}

4.3.2. StrCompare(S,T)

比较操作。若S>T，则返回值>0;若S=T，则返回值=0;若S<T，则返回值<0。

int StrCompare(SString s,SString T){
  for(int i=0;i<=S.length&&i<=T.length){
    if(S.ch[i]!=T.ch[i]){
      return S.ch[i]-T.ch[i];
    }
  }
  return S.length-T.length;
}

4.3.3. Index(S,T)

定位操作。若主串S中存在与串T值相同的子串，则返回它在主串S中第一次出现的位置;否则函数值为0。

int Index(SString S,SString T){
  int i=1,n=StrLength(S),m=Strlength(T);
  SString sub;
  //最多对比 n-m+1 个子串
  while(i<=n-m+1){
    //取出从位置i开始，⻓度为m的子串
    SubString(sub,S,i,m);
    //子串和模式串对比，若不匹配，则匹配下一个子串
    if(StrCompare(sub,T)!=0){
      ++i;
    }else{
      //返回子串在主串中的位置
      return i;
    }
  }
  //S中不存在与T相等的子串
  return 0;
}

5. 模式匹配

主串：‘嘿嘿嘿红红火火恍恍惚惚嗨皮开森猴开森笑出猪叫哈哈哈哈嗨森哈哈哈哈哈哈嗝’

子串：‘笑出猪叫’

子串——主串的一部分，一定存在

模式串——不一定能在主串中找到

字符串模式匹配：在主串中找到与模式串相同的子串，并返回其所在位置。

5.1. 朴素模式匹配算法

将主串中与模式串长度相同的子串搞出来，挨个与模式串对比

当子串与模式串某个对应字符不匹配时，就立即放弃当前子串，转而检索下一个子串

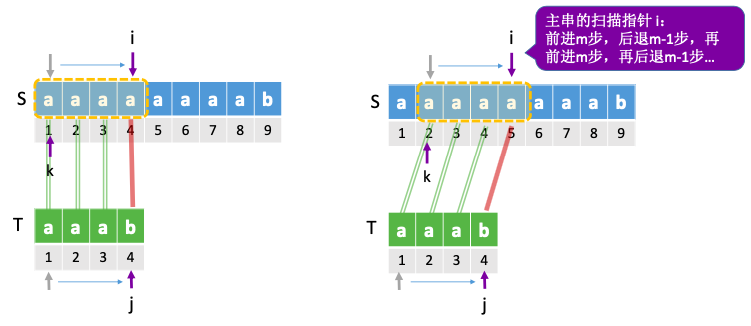
主串⻓度为n，模式串⻓度为 m 最多对比 n-m+1 个子串

朴素模式匹配算法：将主串中所有⻓度为m的子串依次与模式串对比，直到找到一个完全匹配的子串，或所有的子串都不匹配为止。最多对比 n-m+1 个子串

int Index(SString S,SString T){
  int k=1;
  int i=1; 
  int j=1;
  while(i<=S.length&&j<=T.length){
    if(S.ch[i]==T.ch[j]){
      i++;
      j++;
    }else{
      k++;
      i=k; //i=i-j+2;
      j=1;
    }
  }
  if(j>T.length){
    return k;//i-T.length
  }else{
    return 0;
  }
}

若模式串长度为m,主串长度为n，很多时候，n >> m

匹配成功最好 = O(m)

匹配失败最好 = O(n-m+1) = O(n) 每次模式串第一个字符就不匹配，长度为n的主串有n-m+1个长度为m的子串

匹配失败最坏 = O(m(n-m+1)) = O(nm)，每次模式串前m-1个字符匹配，只有第m个字符不匹配，长度为n的主串每次需要回溯n-m+1次

朴素模式匹配算法的缺点: 当某些子串与模式串能部分匹配时，主串的扫􏰁指针 i 经常回溯，导致时间开销增加

5.2. KMP算法

由D.E.Knuth，J.H.Morris和V.R.Pratt􏰀出，因此称为 KMP算法

已匹配相等的序列就是模式串的某个前缀，因此每次回溯就是模式串与模式串某个前缀在比较，这种频繁的重复比较是效率低的原因所在，当匹配到某个字符不等时，滑到已匹配相等的前缀和模式串若有首尾重合位置，对齐它们，对齐部分显然不需要再比较，下一步直接从主串的当前位置继续比较。

使其区别与朴素模式匹配算法，主串指针不回溯

5.2.1. 前后缀，部分匹配值

串的前缀：包含第一个字符，且不包含最后一个字符的子串

串的后缀：包含最后一个字符，且不包含第一个字符的子串

部分匹配值：字符串的前缀和后缀的最长相等前后缀长度

对于’ababa’：

‘a’ 前缀和后缀为空集，最长相等前后缀长度为0
‘ab’ 前缀为{a}，后缀为{b}，{a} $⋂$ {b}= $ϕ$ ，最长相等前后缀长度为0
‘aba’ 前缀为{a,ab}，后缀为{a,ba}，{a,ab} $⋂$ {a,ba}={a} ，最长相等前后缀长度为1
‘abab’ 前缀为{a,ab,aba}，后缀为{b,ab,bab}，{a,ab,aba} $⋂$ {b,ab,bab}={ab} ，最长相等前后缀长度为2
‘ababa’ 前缀为{a,ab,aba,abab}，后缀为{a,ba,aba,baba}，{a,ab,aba,abab} $⋂$ {a,ba,aba,baba}={aba} ，最长相等前后缀长度为3

故字符串’ababa’的部分匹配值为00123

5.2.2. next数组

编号	1	2	3	4	5
S	a	b	c	a	c
PM	0	0	0	1	0

已知：右移动位数=已匹配的字符数-对应的部分匹配值

写成：Move = (j-1)-PM[j-1];

PM表右移一位，元素匹配失败时，直接看自己的部分匹配值，得到next数组

编号	1	2	3	4	5
S	a	b	c	a	c
next	-1	0	0	0	1

第一个元素以-1填充，因为若第一个元素匹配失败，需要子串向右移动一位，不需要计算子串移动位数

最后一个元素在右移过程中溢出，其部分匹配值时其下一个元素使用的，显然已没有下一个元素，故可以舍去。

改写：Move=(j-1)-next[j];

指针j：j=j-Move=next[j]+1;

将next[j]整体+1，则j=next[j]，next[j]表示在子串的第j个字符与主串发生失配时，跳到子串的next[j]位置重新与主串当前位置进行比较。

当模式串的第 j 个字符匹配失败时，令模式串跳到 next[j] 再继续匹配

当第j个字符匹配失败，由前 1~j-1 个字符组成的串记为S，则: next[j]=S的最长相等前后缀长度+1

特别地，next[1]=0

序号j	1	2	3	4	5	6
模式串	a	b	a	b	a	a
next[j]	0	1	1	2	3	4

当模式串第一个字符与主串的当前字符比较不相等时，next[1]=0，表示模式串应右移一位，主串当前指针后移一位，再和模式串的第一个字符进行比较。
当主串的第i个字符与模式串的第j个字符失配时，主串i不回溯，则假定模式串的第k个字符与主串的第i个字符比较，k值应该满足条件1<k<j且’p₁…p_k-1‘=’p_j-k+1…p_j-1‘，k为模式串的下次比较位置。k值可能有多个，为了不使向右移动丢失可能的匹配，右移距离应该取最小，由于j-k表示右移距离，所以取max(k)。
除了上面两种情况外，发生失配时，主串指针i不回溯，在最坏情况下，模式串从第一个字符开始与主串的第i个字符进行比较。

void get_Next(SString T,int next[]){
  int i=1;
  int j=0;
  next[1]=0;
  while(i<=T.length){
    if(j==0||T.ch[i]==T.ch[j]){
      i++;
      j++;
      next[i]=j;
    }else{
      j=next[j];
    }
  }
}

5.2.3. KMP算法

int Index_KMP(SString S,SString T,int next[]){
  int i=1;
  int j=1;
  get_Next(T,next);
  while(i<=S.length&&j<=T.length){
    if(j==0||S.ch[i]==T.ch[j]){
      i++;
      j++;
    }else{
      j=next[j];
    }
  }
  if(j>T.length){
    return i-T.length;
  }else{
    return 0;
  }
}

最坏时间复杂度 O(m+n)

其中，求 next数组时间复杂度 O(m)

模式匹配过程最坏时间复杂度 O(n)

5.2.4. KMP算法优化

减少无意义的对比

当子串和模式串不匹配时j=nextval[j];

序号j	1	2	3	4	5	6
模式串	a	b	a	b	a	a
next[j]	0	1	1	2	3	4
nextval[i]	0	1	0	1	0	4

//nextval数组的求法: 
//先算出next数组 
//先令nextval[1]=0
for (int j=2; j<=T.length; j++) {
  if(T.ch[next[j]]==T.ch[j]){
    nextval[j]=nextval[next[j]];
  }
  else{
		nextval[j]=next[j];
  }
}

王道版本

void get_Next(SString T,int next[]){
  int i=1;
  int j=0;
  next[1]=0;
  while(i<=T.length){
    if(j==0||T.ch[i]==T.ch[j]){
      i++;
      j++;
      if(T.ch[i]!=T.ch[j]){
      	nextval[i]=j;
      }else{
        nextval[i]=nextval[j];
      }
    }else{
      j=nextval[j];
    }
  }
}

5.3. 总结

朴素模式匹配算法的缺点：当某些子串与模式串能部分匹配时，主串的扫描指针 i 经常回溯，导致时间开销增加。最坏时间复杂度O(nm)

KMP算法：当子串和模式串不匹配时，主串指针 i 不回溯，模式串指针 j=next[j]，算法平均时间复杂度：O(n+m)

next数组手算方法：当第j个字符匹配失败，由前 1~ j-1 个字符组成的串记为S，则: next[j]=S的最长相等前后缀长度+1。特别地，next[1]=0

W.T.的博客

数据结构与算法分析-串