1. 基本初等函数
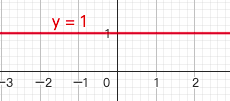
1.1. 常数 y = A
A为常数
图形是平行与x轴的水平直线
偶函数
1.2. 幂函数 $y = x^a$
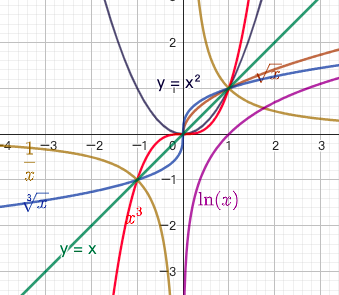
- 当 x>0时,y=x 与 $y = \sqrt{x}$,$y = \sqrt[3]{x} $,$y=\ln x$ 具有相同的单调性,与 $y=\frac{1}{x}$具有相反的单调性
- 见到 $\sqrt{x},\sqrt[3]{x}$ ,可用 x 来研究最值
- 见到 |x|,$|x|=\sqrt{x^2}$,可用$x^2$ 来研究最值
- 见到 $\mathop\nolimits_1\mathop\nolimits_2\mathop\nolimits_3$,可用 $\ln(\mathop\nolimits_1\mathop\nolimits_2\mathop\nolimits_3)=\ln\mathop\nolimits_1+\ln\mathop\nolimits_2+\ln\mathop\nolimits_3$ 来研究最值
- 见到 $\frac{1}{x}$,可用 x 来研究最值,$\frac{1}{x}$最大值则x最小值,$\frac{1}{x}$最小值则x最大值
1.3. 指数 $y = a^x$
- a>0,a$\ne$1
- $x \in (-\infty,+\infty),y \in (0,+\infty)$
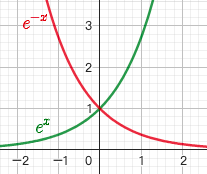
- $a^0$ = 1
- 当 a>1 时,图像单调递增,当 0<a<1时,图像单调递减
- a>1时,$\lim_{x \to -\infty} a^x = 0, \lim_{x \to +\infty} a^x = +\infty$
1.4. 对数函数 $y=\log_{a}x$
- a>0,a$\ne$1
- 是 $y=a^x$ 的反函数
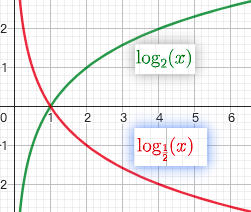
- 当 a>1 时,图像单调递增,当 0<a<1时,图像单调递减
- $\lim_{x \to 0^+} \ln x = -\infty, \lim_{x \to +\infty} \ln x = +\infty$
- $x = e^{\ln x}, u^v = e^{\ln u^v} = e^{v\ln u}$
1.5. 三角函数
1.5.1. 正弦函数 $y=sinx$
- $x \in (-\infty,+\infty),y \in [-1,1]$
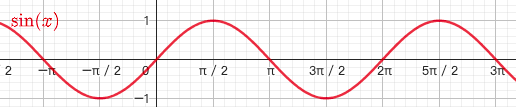
奇函数
最小正周期为$2\pi$
一拱面积
- $\int_{0}^{\pi}sinx = 2$
- $\int_{\frac{\pi}{4}}^{\frac{3\pi}{4}}sinx = \sqrt2$
- $\int_{0}^{\frac{\pi}{4}}sinx = 1-\frac{\sqrt2}{2}$
1.5.2. 余弦函数 $y=cosx$
- $x \subset (-\infty,+\infty),y \subset [-1,1]$
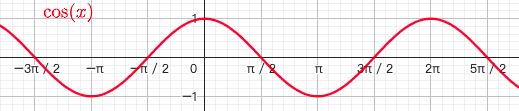
- 偶函数
- 最小正周期为$2\pi$
1.5.3. 正切函数 $y=tanx$
$y=tanx = \frac{sinx}{cosx}$
$x\ne k\pi+\frac{\pi}{2}$
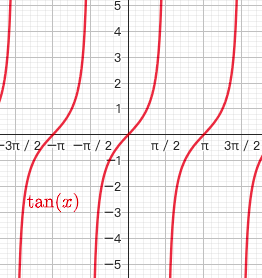
- 奇函数
- 最小正周期为$\pi$
1.5.4. 余切函数 $y=cotx$
- $y=cotx = \frac{cosx}{sinx}$
- $x\ne k\pi$
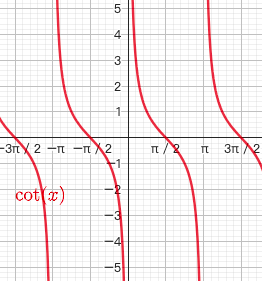
- 奇函数
- 最小正周期为$\pi$
1.5.5. 正割函数 $y=secx$
- $y=secx=\frac{1}{cosx}$
- $x\ne k\pi+\frac{\pi}{2}$
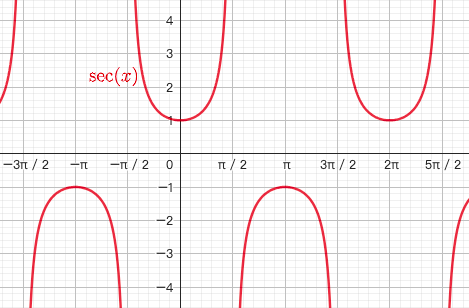
- 偶函数
- 最小正周期为$2\pi$
1.5.6. 余割函数 $y=cscx$
- $y=cscx=\frac{1}{sinx}$
- $x\ne k\pi$
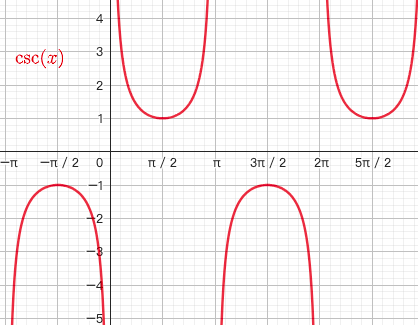
- 奇函数
- 最小正周期为$2\pi$
1.6. 反三角函数
1.6.1. 反正弦函数 $y=arcsinx$
- $x \in [-1,1],y \in [-\frac{\pi}{2},\frac{\pi}{2}]$
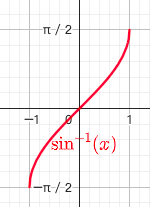
- 奇函数
- 图像单调递增
1.6.2. 反余弦函数 $y=arccosx$
- $x \in [-1,1],y \in [0,\pi]$
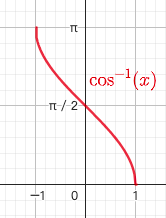
1.6.3. 反正切函数 $y=arctanx$
- $x \in R,y \in [-\frac{\pi}{2},\frac{\pi}{2}]$
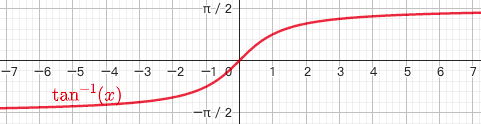
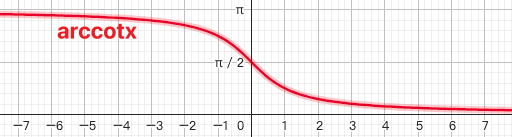
1.6.4. 反余切函数 $y=arccotx$
$x \in R,y \in [0,\pi]$
2. 初等函数
- 由基本初等函数经有限次的四则运算,以及有限次的复合步骤所构成的并且可以由一个式子所表示的函数称为初等函数
2.1. 孤立点
- 初等函数的定义域可以是一个区间,也可以是几个区间的并集,还可以是一些孤立的点
$y=\sqrt{coś\pi x - 1},x=0,\pm1,\pm2,…$
2.2. 幂指函数 $y=x^x$
- x>0
- $y=x^x=e^{\ln x^x} = e^{x\ln x}$
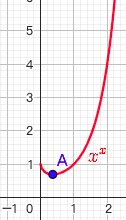
- $A(\frac{1}{e},e^{\frac{1}{e}})$ 为极小值点,也为最小值点
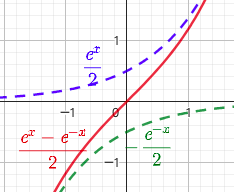
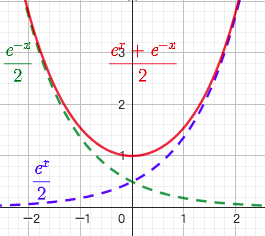
2.3. 双曲正弦函数 $y=shx$
$y = shx=\frac{e^x-e^{-x}}{2}$
$x \in R$
奇函数,单调递增
图像在第一象限内接近于曲线 $y=e^x$,在第三象限接近于曲线$y=-\frac{e^{-x}}{2}$
2.4. 双曲余弦函数 $y=chx$
$y=chx=\frac{e^x+e^{-x}}{2}$
$x \in R$
偶函数
图像在第一象限内接近于曲线 $y=\frac{e^x}{2}$,在第三象限接近于曲线$y=\frac{e^{-x}}{2}$
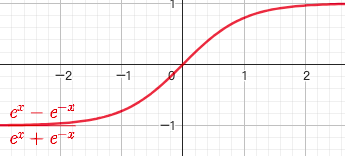
2.5. 双曲正切函数 $y=thx$
$y = thx=\frac{e^x-e^{-x}}{e^x+e^{-x}}$
$x \in R$
奇函数,单调递增
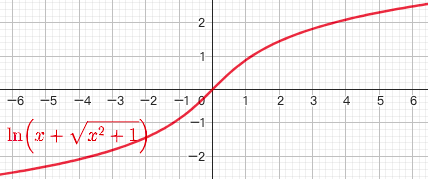
2.6. 反双曲正弦函数 $y=arshx$
$y=arshx = \ln (x+\sqrt{x^2+1})$
$x \in R$
奇函数,单调递增
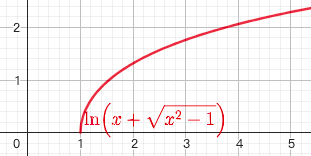
2.7. 反双曲余弦函数 $y=archx$
$y= archx = \ln (x+\sqrt{x^2-1})$
$x \in [0,+\infty], y \in [1,+\infty]$
单调递增
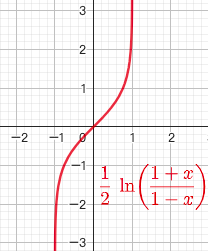
2.8. 反双曲正切函数 $y=arthx$
$y= arthx = \frac{1}{2}\ln \frac{1+x}{1-x}$
$x \in (-1,1), y \in R$
奇函数,单调递增
3. 分段函数
- 在自变量的不同变化范围中,对应法则用不同式子来表示的函数称为分段函数
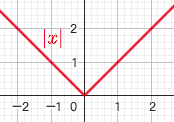
3.1. 绝对值函数 $y=\left |x \right | $
- $y=\left | x \right | = \begin{cases} x & x\ge 0 \ -x & x<0 \end{cases}$
3.2. 符号函数 $y=sgnx$
$y=sgnx = \begin{cases} 1 & x>0 \ 0 &x=0 \ -1 & x<0 \end{cases}$
任何一个 $x=|x|sgnx$
3.3. 取整函数 $y= \left [ x \right ] $
- 不超过x的最大整数称为x的整数部分
- $x-1\lt [x] \le x$
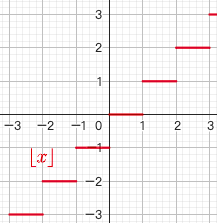
- $\lim_{x \to 0^-} [x]= -1, \lim_{x \to 0^+} [x]= 0$
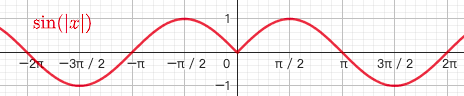
3.4. $y=sin|x|$
- 偶函数
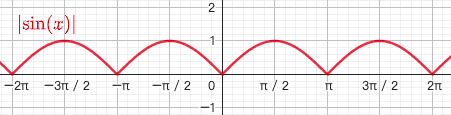
3.5. $y=|sinx|$
- 偶函数
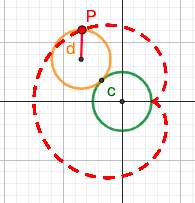
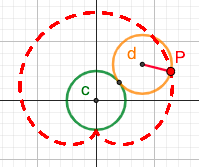
4. 笛卡尔心形线(Cardioid)
4.1. $r = a(1-cos\theta)$
a>0
定圆C,动圆d,定圆c的半径等于动圆d的半径
要求圆c与圆d相切,选取切点P为外摆线轨迹原点,当动圆d绕着定圆c的外侧逆时针滚动时,点P形成的轨迹就是外摆线
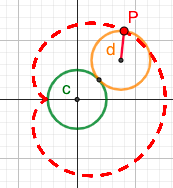
4.2. $r = a(1+cos\theta)$
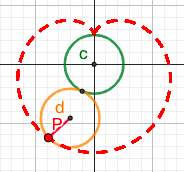
4.3. $r = a(1-sin\theta)$
4.4. $r = a(1+sin\theta)$
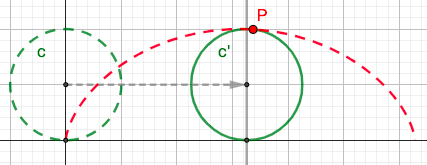
5. 平摆线
- 圆c沿定直线x轴作纯滚动,圆c圆周上一个定点的轨迹叫做摆线
$\left{\begin{matrix}
x =r(t-sint)
\y = r(1-cost)
\end{matrix}\right.$
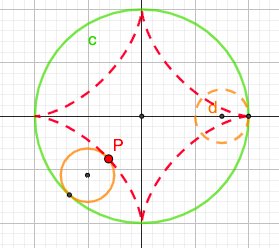
6. 内摆线
- 大圆c半径为r,小圆d半径为r/4,圆d在圆c内部作纯滚动,圆d上任一点P的轨迹称为星形线
$\left{\begin{matrix}
x = rcos^3t
\y = rsin^3t
\end{matrix}\right.$
直角坐标系:
$x^{\frac{2}{3}} + y^{\frac{2}{3}} = r^{\frac{2}{3}}$
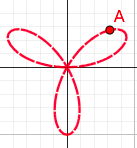
7. 三叶玫瑰线 $r=asin3\theta$
a>0
8. 阿基米德螺线 $r=a\theta$
- a>0,$\theta\geqslant0$
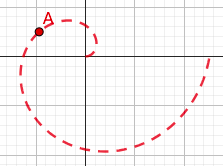
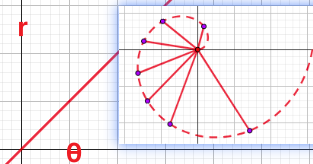
- 用直角坐标系观点画极坐标系下的图像
- y=x => r=$\theta$,从方程角度看问题,两个方程的形式相同,只是表示变量的字母不同而已,但是坐标系不同,曲线完全不同
- 单看直角坐标系下的r=f($\theta$)图像,r是随着$\theta$ 的增大而增大的
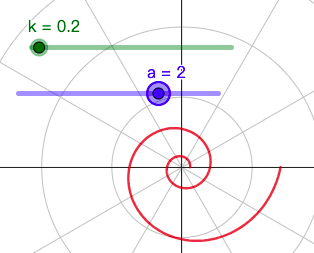
9. 对数螺线 $y=ae^{k\theta}$
- a>0,k>0
- 当 $\theta$ 由0逐渐增大时,r由a逐渐增大,当 $\theta$ 无限制增大,r也随之无限制增大;当 $\theta$ 由0逐渐减小,r由a逐渐减小,但r却永远保持正值,当 $\theta$ 由0无限制减小,r也随之无限制接近于0
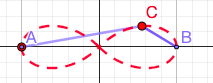
10. 伯努利双纽线
- 设直线AB的长度为2a(a>0),若有一动点C(x,y)满足|AC|·|BC|=$a^2$,那么点C的轨迹就是双纽线
10.1. $r^2=2a^2cos2\theta$
$\theta \in [-\frac{\pi}{4}, \frac{\pi}{4}] \cup [\frac{3\pi}{4}, \frac{5\pi}{4}]$
直角坐标系
$(x^2+y^2)^2 = a^2(x^2-y^2)$
10.2. $r^2=2a^2sin2 \theta$
$\theta \in [0, \frac{\pi}{2}] \cup [\pi, \frac{3\pi}{2}]$
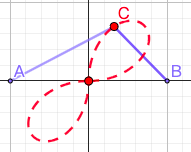
直角坐标系
$(x^2+y^2)^2 = 2a^2xy$