栈[顺序栈，链栈]，队列[循环队列，链式队列]

视频讲解，习题讲解，思维导图，PPT资源

链接: https://pan.baidu.com/s/1Fwji3dgqIhU6C4BzN13bBQ 密码: e4t2

1. 栈(Stack) 基本概念

1.1. 栈的定义

线性表是具有相同数据类型的n(n≥0)个数据元素的有限序列，其中n为表长，当n = 0时线性表是一个空表。若用L命名线性表，则其一般表示为 L = (a₁, a₂, … , a_i, a_i+1, … , a_n)

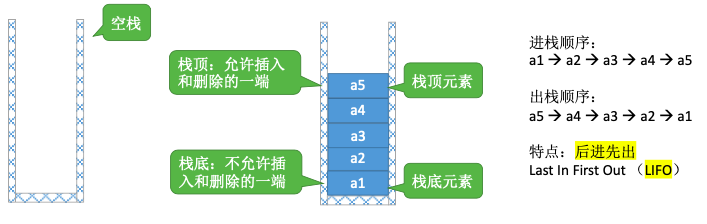
栈(Stack)是只允许在一端进行插入或删除操作的线性表

逻辑结构：与普通线性表相同

数据的运算：插入、删除操作有区别

重要术语：栈顶、栈底、空栈

1.2. 栈的基本操作

###创、销

InitStack(&S)：初始化栈。构造一个空栈 S，分配内存空间。

DestroyStack(&S):销毁栈。销毁并释放栈 S 所占用的内存空间。

1.2.1. 增、删

Push(&S,x)：进栈，若栈S未满，则将x加入使之成为新栈顶。

Pop(&S,&x)：出栈，若栈S非空，则弹出栈顶元素，并用x返回。删除栈顶元素

GetTop(S, &x)：读栈顶元素。若栈 S 非空，则用 x 返回栈顶元素。不删除栈顶元素，栈的使用场景中大多只访问栈顶元素

1.2.2. 其他常用操作

StackEmpty(S)：判断一个栈 S 是否为空。若S为空，则返回true，否则返回false。

1.3. 栈的常考题型

进栈顺序:

a->b->c->d->e

有哪些合法的出栈顺序?

n个不同元素进栈，出栈元素不同排列的个数为 $\frac{1}{n+1}$C$_{2n}^{n}$

上述公式称为卡特兰(Catalan)数，可采用数学归纳法证明(不要求掌握)。

$\frac{1}{5+1}$C$_{10}^{5}$=$\frac{10∗9∗8∗7∗6}{6∗5∗4∗3∗2∗1}$ =42

1.4. 顺序栈

1.4.1. 顺序栈的定义

//定义栈中元素的最大个数
#define MaxSize 10
typedef struct{
  	//静态数组存放栈中元素
  	ElemType data[MaxSize];
  	//栈顶指针
  	int top;
}SqStack;

void testStack(){
  //声明一个顺序栈(分配空间)
  SqStack s;
}

图解：

1.4.2. 初始化操作

top指向栈顶指针

#define MaxSize 10
typedef struct{
  	ElemType data[MaxSize];
  	int top;
}SqStack;

//初始化
void InitStack(SqStack &S){
  //初始化栈顶指针
  S.top = -1;
}

1.4.3. 判空操作

#define MaxSize 10
typedef struct{
  	ElemType data[MaxSize];
  	int top;
}SqStack;

bool StackEmpty(SqStack S){
  if(S.top == -1){
    return true;
  }else{
    return false;
  }
}

1.4.4. 栈满判断

#define MaxSize 10
typedef struct{
  	ElemType data[MaxSize];
  	int top;
}SqStack;

bool StackFull(SqStack S){
  if(S.top==MaxSize-1){
    return true;
  }else{
    return false;
  }
}

1.4.5. 进栈操作

#define MaxSize 10
typedef struct{
  	ElemType data[MaxSize];
  	int top;
}SqStack;

//进栈
bool Push(SqStack &S, ElemType x){
  if(S.top==MaxSize-1){
    return false;
  }
  //top指向栈顶
  S.data[++S.top]=x;
  return true;
}

1.4.6. 出栈操作

#define MaxSize 10
typedef struct{
  	ElemType data[MaxSize];
  	int top;
}SqStack;

//进栈
bool Pop(SqStack &S, ElemType &x){
  if(S.top==-1){
    return false;
  }
  x = S.data[S.top--];
  return true;
}

1.4.7. 读栈顶元素

#define MaxSize 10
typedef struct{
  	ElemType data[MaxSize];
  	int top;
}SqStack;

//进栈
bool GetTop(SqStack &S, ElemType x){
  if(S.top==-1){
    return false;
  }
  x = S.data[S.top];
  return true;
}

1.4.8. 若top指向栈顶后一个位置

//栈空
S.top==0;
//栈满
S.top==MaxSize;
//进栈
S.data[S.top++]=x;
//出栈
x = S.data[--S.top];
//栈顶
x = S.data[S.top-1];

1.5. 共享栈

利用栈底位置相对不变的特性，让两个顺序栈共享一个一维空间，将两个栈的栈底分别设置在共享空间的两端，两个栈顶向共享空间的中间延伸。采用共享栈的好处是节省存储空间，降低发生上溢的可能

1.5.1. 共享栈的定义

#define MaxSize 10
typedef struct{
  ElemType data[MaxSize];
  //0号栈栈顶指针
  int top0;
  //1号栈栈顶指针
  int top1;
}ShStack;

1.5.2. 初始化操作

#define MaxSize 10
typedef struct{
  ElemType data[MaxSize];
  //0号栈栈顶指针
  int top0;
  //1号栈栈顶指针
  int top1;
}ShStack;

//初始化栈顶指针
void InitStack(ShStack &S){
  S.top0=-1;
  S.top1=MaxSize;
}

1.5.3. 栈满判断

1	S.top0 + 1==S.top1;

1.6. 链栈

用链式存储方式实现的栈

1.6.1. 链栈定义

typedef struct Linknode{
  //数据域
  ElemType data;
  //指针域
  struct Linknode *next;
}*LiStack;

1.6.2. 两种实现方式

1.6.2.1. 带头结点

1 2	LiStack s; s->next == NULL;

1.6.2.2. 不带头结点

1 2	LiStack s; s == NULL;

1.6.3. 进栈操作(带头结点)

typedef struct Linknode{
  ElemType data;
  struct Linknode *next;
}*LiStack;

//等同于链表的头插法
bool Push(LiStack &S,ElemType x){
  Linknode *e = (Linknode*)malloc(sizeof(Linknode));
  //栈空间分配失败
  if(e==NULL){
    return false;
  }
  e->data = x;
  e->next = S->next;
  S->next = e;
  return true;
}

1.6.4. 出栈操作(带头结点)

typedef struct Linknode{
  ElemType data;
  struct Linknode *next;
}*LiStack;

bool Pop(LiStack &S,ElemType &x){
  //栈空
  if(S->next==NULL){
    return false;
  }
  x = S->data;
  S = S->next;
  return true;
}

1.7. 栈的应用

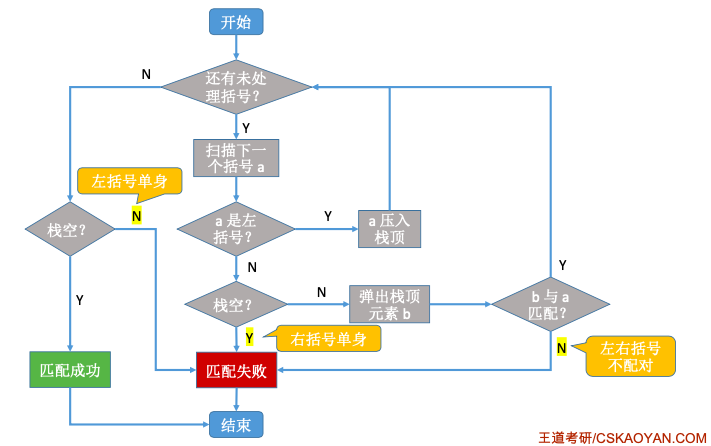
1.7.1. 括号匹配

依次扫描所有字符，遇到左括号入栈，遇到右括号则弹出栈顶元素检查是否匹配。

匹配失败情况:

左括号单身
右括号单身
左右括号不匹配

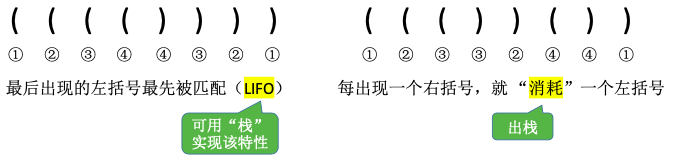
判断括号是否匹配流程图：

代码实现

#define MaxSize 10
typedef struct{
  char data[MaxSize];
  int top;
}SqStack;

//初始化栈
void InitStack(SqStack &S)

//判断栈是否为空
bool StackEmpty(SqStack S)

//新元素入栈
bool Push(SqStack &S,char x)

//栈顶元素出栈，用x返回
bool Pop(SqStack &S,char &x)
  
  
bool bracketCheck(char str[],int length){
  SqStack S;
  InitStack(S);
  for(int i=0;i<length;i++){
    if(str[i]=='{'||str[i]=='['||str[i]=='('){
      Push(S,str[i]);
    }
    else{
      if(StackEmpty(S)){
        return false;
      }
      char topElem;
      Pop(S,topElem);
      if(str[i]==')'&&topElem!='('){
        return false;
      }
      if(str[i]==']'&&topElem!='['){
        return false;
      }
      if(str[i]=='}'&&topElem!='{'){
        return false;
      }
    }
  }
  return StackEmpty(S);
}

1.7.2. 表达式求值

Reference: Wikipedia ——Reverse Polish notation

Reverse Polish notation(逆波兰表达式 = 后缀表达式)

Polish notation(波兰表达式 = 前缀表达式)

中缀表达式(运算符在两个操作数中间)： a+b

后缀表达式(运算符在两个操作数后面)： ab+

前缀表达式(运算符在两个操作数前面)： +ab

1.7.2.1. 中缀表达式转后缀表达式(手算)

确定中缀表达式中各个运算符的运算顺序
选择下一个运算符，按照【左操作数右操作数运算符】的方式组合成一个新的操作数
如果还有运算符没被处理，就继续【2】

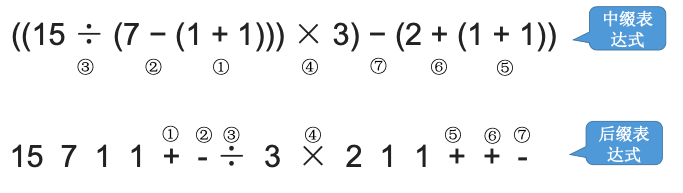
运算顺序不唯一，因此对应的后缀表达式也不唯一

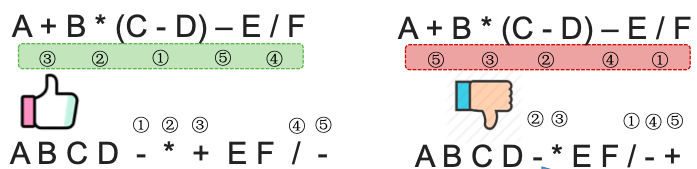
私房菜：“左优先”原则，不要FreeStyle，保证手算和机算结果相同“左优先”原则：只要左边的运算符能先计算，就优先算左边的

1.7.2.2. 后缀表达式的计算

从左往右扫描下一个元素，直到处理完所有元素
若扫描到操作数则压入栈，并回到【1】；否则执行【3】 注意：先出栈的是“右操作数”
若扫描到运算符，则弹出两个栈顶元素，执行相应运算，运算结果压回栈顶，回到【1】

1.7.2.3. 中缀表达式转后缀表达式(机算)

初始化一个栈，用于保存暂时还不能确定运算顺序的运算符。从左到右处理各个元素，直到末尾。可能遇到三种情况：

遇到操作数。直接加入后缀表达式。
遇到界限符。遇到“(”直接入栈；遇到“)”则依次弹出栈内运算符并加入后缀表达式，直到弹出“(”为止。注意：“(”不加入后缀表达式。
遇到运算符。依次弹出栈中优先级(\*优先级高于+ -)高于或等于当前运算符的所有运算符，并加入后缀表达式，若碰到“(” 或栈空则停止。之后再把当前运算符入栈。

按上述方法处理完所有字符后，将栈中剩余运算符依次弹出，并加入后缀表达式。

优先级：栈内$\geq$栈外时，栈内元素出栈

	(	* /	+ -	)
栈内	1	5	3	6
栈外	6	4	2	1

1.7.2.4. 中缀表达式的计算(用栈实现)

用栈实现中缀表达式的计算：

初始化两个栈，操作数栈和运算符栈

若扫描到操作数，压入操作数栈

若扫描到运算符或界限符，则按照“中缀转后缀”相同的逻辑压入运算符栈(期间也会弹出运算符，每当弹出一个运算符时，就需要再弹出两个操作数栈的栈顶元素并执行相应运算，运算结果再压回操作数栈)

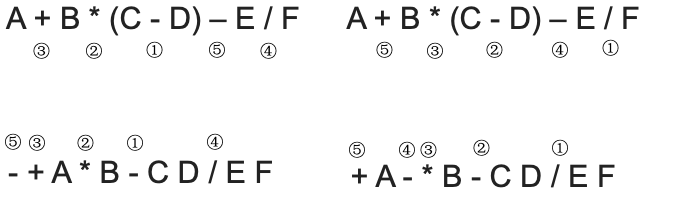
1.7.2.5. 中缀表达式转前缀表达式(手算)

确定中缀表达式中各个运算符的运算顺序
选择下一个运算符，按照【运算符左操作数右操作数】的方式组合成一个新的操作数
如果还有运算符没被处理，就继续【2】

“右优先”原则：只要右边的运算符能先计算，就优先算右边的

1.7.2.6. 前缀表达式的计算

从右往左扫描下一个元素，直到处理完所有元素
若扫描到操作数则压入栈，并回到【1】;否则执行【3】 注意:先出栈的是“左操作数”
若扫描到运算符，则弹出两个栈顶元素，执行相应运算，运算结果压回栈顶，回到【1】

1.7.3. 递归

可以把原始问题转换为属性相同，但规模较小的问题

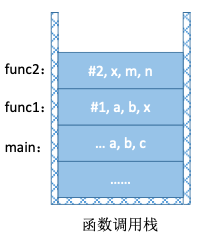
1.7.3.1. 函数调用背后的过程

void main(){
  int a = 1;
  int b = 2;
  int c = 3;
  func1(a,b);
  c = a+b; //#1
}

void func1(int a,int b){
  int x;
  func2(x);
  x = x+10086; //#2
}

void func2(int x){
  int m,n;
}

函数调用的特点:最后被调用的函数最先执行结束(LIFO)

函数调用时，需要用一个栈存储:

调用返回地址
实参
局部变量

1.7.3.2. 计算正整数的阶乘 n!

factorial (n) = $\left{\begin{matrix}
n*factorial(n-1) , n>1 (递归表达式)& \
1, n=1 (边界条件)& \
1, n=0 (边界条件)&
\end{matrix}\right.$

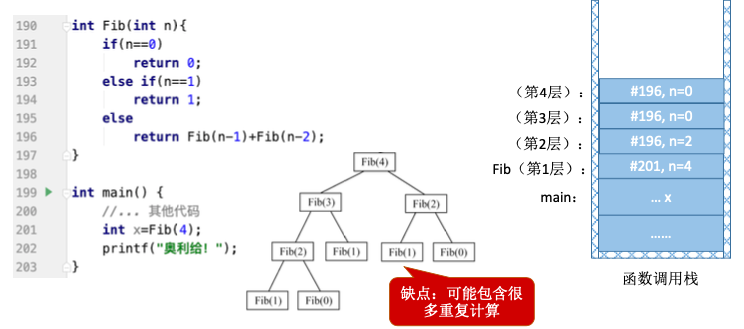
1.7.3.3. 求斐波那契数列

Fib(n)=$\left{\begin{matrix}
Fib(n-1)+Fib(n-2) , n>1 & \
1, n=1 & \
0, n=0 &
\end{matrix}\right.$

2. 队列(Queue)的基本概念

2.1. 队列的定义

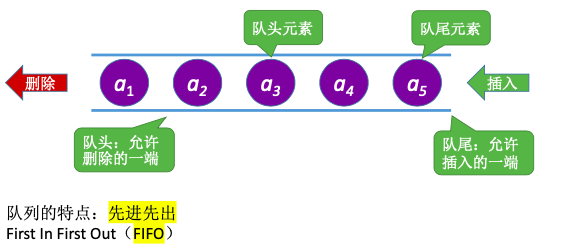
队列(Queue)是只允许在一端进行插入，在另一端删除的线性表

特点：先进入队列的元素先出队

重要术语:队头、队尾、空队列

2.2. 队列的基本操作

InitQueue(&Q)：初始化队列，构造一个空队列Q。

DestroyQueue(&Q)：销毁队列。销毁并释放队列Q所占用的内存空间。

EnQueue(&Q ,x)：入队，若队列Q未满，将x加入，使之成为新的队尾。

DeQueue(&Q ,&x)：出队，若队列Q非空，删除队头元素，并用x返回。删除队头元素

GetHead(Q ,&x)：读队头元素，若队列Q非空，则将队头元素赋值给x。不删除队头元素

其他常用操作:

QueueEmpty(Q)：判队列空，若队列Q为空返回true，否则返回false。

2.3. 队列的顺序实现

#define MaxSize 10
typedef struct{
  //用静态数组存放队列元素
  ElemType data[MaxSize];
  //队头指针，队尾指针
  int front,rear;
}SqQueue;

void testQueue(){
  SqQueue Q;
}

Q.front=0指向队头

Q.rear=0指向队尾后一个元素

2.3.1. 初始化操作

#define MaxSize 10
typedef struct{
  ElemType data[MaxSize];
  int front,rear;
}SqQueue;

void InitQueue(SqQueue &Q){
  Q.rear = Q.front = 0;
}

2.3.2. 判空

#define MaxSize 10
typedef struct{
  ElemType data[MaxSize];
  int front,rear;
}SqQueue;


bool QueueEmpty(SqQueue Q){
  if(Q.rear == Q.front){
    return true;
  }else{
    return false;
  }
}

2.3.3. 循环队列–如何判满

如何判满？Q.rear==MaxSize？

在Q.front+1=Q.rear=Maxsize时，其实是列空的，该如何判断？用循环队列

循环队列：用模运算将存储空间在逻辑上变成“环状”

判满方案有三种：

2.3.3.1. 队尾指针下一个位置是队头

队空：Q.rear==Q.front

队满：Q.front == (Q.rear+1)%MaxSize

入队：Q.data[Q.rear]=x; Q.rear = (Q.rear+1)%MaxSize;

出队：x = Q.data[Q.front]; Q.front = (Q.front+1)%MaxSize;

2.3.3.2. 添加size元素

#define MaxSize 10
typedef struct{
  ElemType data[MaxSize];
  int front,rear;
  //队列元素个数
  int size;
}SqQueue;

初始操作：Q.front=Q.rear=0; Q.size=0；

入队元素：Q.rear++; Q.size++;

元素出队：Q.front++; Q.size–;

队满判断：Q.size==MaxSize-1;

队空判断：Q.size==0;

2.3.3.3. 添加标签位tag

#define MaxSize 10
typedef struct{
  ElemType data[MaxSize];
  int front,rear;
  //最近进行的是添加/删除
  int tag;
}SqQueue;

初始化时，Q.rear=Q.front=0，Q.tag=0

每次删除操作成功时，都令Q.tag=0；

每次插入操作成功时，都令Q.tag=1；

队满判断：Q.rear==Q.front&&tag==1

队空判断：Q.rear==Q.front&&tag==0

入队：Q.rear++; Q.tag=1;

出队：Q.front++; Q.tag=0;

2.3.4. 取队头元素

bool GetHead(SqQueue Q,ElemType &x){
  if(Q.rear==Q.front){
    return false;
  }
  x = Q.data[Q.front];
  return true;
}

2.3.5. 求元素个数

1
2
3

int GetNum(SqQueue Q){
  return (Q.rear+MaxSize-Q.front)%MaxSize;
}

2.3.6. 修改队列指针指向

//指向队头元素
Q.front=0;
//指向队尾元素
Q.rear=MaxSize-1;

//入队
Q.rear = (Q.rear+1)%MaxSize;
Q.data[Q.rear]=x;

//出队
x = Q.data[Q.front];
Q.front=(Q.front+1)%MaxSize;

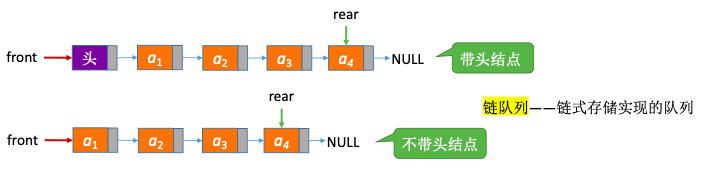
2.4. 队列的链式存储

一个同时带有队头指针和队尾指针的单链表。头指针指向队头，尾指针指向队尾。

typedef struct LinkNode{
  ElemType data;
  struct LinkNode *next;
}LinkNode;

typedef struct{
  LinkNode *front,*next;
}LinkQueue;

2.4.1. 初始化操作

2.4.1.1. 带头结点

void InitQueue(LinkQueue &Q){
  Q.front=Q.rear=(LinkNode*)malloc(sizeof(LinkNode));
  Q.front->next=NULL;
}

2.4.1.2. 不带头结点

1
2
3

void InitQueue(LinkQueue &Q){
  Q.front=Q.rear=NULL;
}

2.4.2. 判空

bool Empty(LinkQueue Q){
  if(Q.front==Q.rear){
    return true;
  }else{
    return false;
  }
}

2.4.3. 入队

2.4.3.1. 带头结点

void EnQueue(LinkQueue &Q,ElemType x){
  LinkNode *s = (LinkNode*)malloc(sizeof(LinkNode));
  s->data=x;
  s->next=NULL;
  //指针尾插法插入到链表中
  Q.rear->next=s;
  Q.rear=s;
}

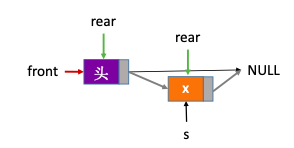
2.4.3.2. 不带头结点

void EnQueue(LinkQueue &Q,ElemType x){
  LinkNode *s = (LinkNode*)malloc(sizeof(LinkNode));
  s->data=x;
  s->next=NULL;
  if(Q.front==NULL){
    Q.front=s;
    Q.rear=s;
  }else{
  	Q.rear->next=s;
  	Q.rear=s;
  }
}

2.4.4. 出队

2.4.4.1. 带头结点

bool DeQueue(LinkQueue &Q,ElemType &x){
  if(Q.front==Q.rear){
    //空队
    return false;
  }
  LinkNode *p=Q.front->next;
  //用变量x返回队头元素
  x=p->data;
  //修改头结点的next指针
  Q.front->next=p->next;
  //若为最后一个结点出队
  if(Q.rear==p){
    //修改rear指针
    Q.rear=Q.front;
  }
  //释放结点空间
  free(p);
  return true;
}

2.4.4.2. 不带头结点

bool DeQueue(LinkQueue &Q,ElemType &x){
  if(Q.front==Q.rear){
    //空队
    return false;
  }
  LinkNode *p=Q.front->next;
  //用变量x返回队头元素
  x=p->data;
  //修改头结点的指针
  Q.front=p->next;
  //若为最后一个结点出队
  if(Q.rear==p){
    //修改front,rear指针
    Q.rear=NULL;
    Q.front=NULL;
  }
  //释放结点空间
  free(p);
  return true;
}

2.4.5. 队满

顺序存储——预分配的空间耗尽时队满

链式存储——一般不会队满，除非内存不足

2.5. 双端队列

只允许从两端插入、两端删除的线性表

若只使用其中一端的插入、删除操作，则效果等同于栈

2.5.1. 双端队列形式

2.5.2. 判断输出序列合法性

若数据元素输入序列为 1,2,3,4，则哪些输出序列是合法的，哪些是非法的?

𝐴$_{4}^{4}$= 4! = 24

2.5.2.1. 对于栈

以1开头	以2开头	以3开头	以4开头
`1,2,3,4`	`2,1,3,4`	3,1,2,4	4,1,2,3
`1,2,4,3`	`2,1,4,3`	3,1,4,2	4,1,3,2
`1,3,2,4`	`2,3,1,4`	`3,2,1,4`	4,2,1,3
`1,3,4,2`	`2,3,4,1`	`3,2,4,1`	4,2,3,1
1,4,2,3	2,4,1,3	3,4,1,2	4,3,1,2
`1,4,3,2`	`2,4,3,1`	`3,4,2,1`	`4,3,2,1`

卡特兰数：14种合法出栈序列

$\frac{1}{n+1}$C${2n}^{n}$ = $\frac{1}{4+1}$C${8}^{4}$=14

2.5.2.2. 输入受限的双端队列

栈中合法的序列，双端队列中一定也合法

以1开头	以2开头	以3开头	以4开头
`1,2,3,4`	`2,1,3,4`	`3,1,2,4`	`4,1,2,3`
`1,2,4,3`	`2,1,4,3`	`3,1,4,2`	`4,1,3,2`
`1,3,2,4`	`2,3,1,4`	`3,2,1,4`	4,2,1,3
`1,3,4,2`	`2,3,4,1`	`3,2,4,1`	4,2,3,1
`1,4,2,3`	`2,4,1,3`	`3,4,1,2`	`4,3,1,2`
`1,4,3,2`	`2,4,3,1`	`3,4,2,1`	`4,3,2,1`

2.5.2.3. 输出受限的双端队列

以1开头	以2开头	以3开头	以4开头
`1,2,3,4`	`2,1,3,4`	`3,1,2,4`	`4,1,2,3`
`1,2,4,3`	`2,1,4,3`	`3,1,4,2`	4,1,3,2
`1,3,2,4`	`2,3,1,4`	`3,2,1,4`	`4,2,1,3`
`1,3,4,2`	`2,3,4,1`	`3,2,4,1`	4,2,3,1
`1,4,2,3`	`2,4,1,3`	`3,4,1,2`	`4,3,1,2`
`1,4,3,2`	`2,4,3,1`	`3,4,2,1`	`4,3,2,1`

有一个双端队列，输入序列为1，2，3，4，求以下条件的输出序列：

能由输入受限的双端队列得到，但不能由输出受限的双端队列得到的输出序列 4,1,3,2
能由输出受限的双端队列得到，但不能由输入受限的双端队列得到的输出序列 4,2,1,3
不能由输入受限的双端队列得到，也不能由输出受限的双端队列得到的输出序列 4,2,3,1

2.6. 队列的应用

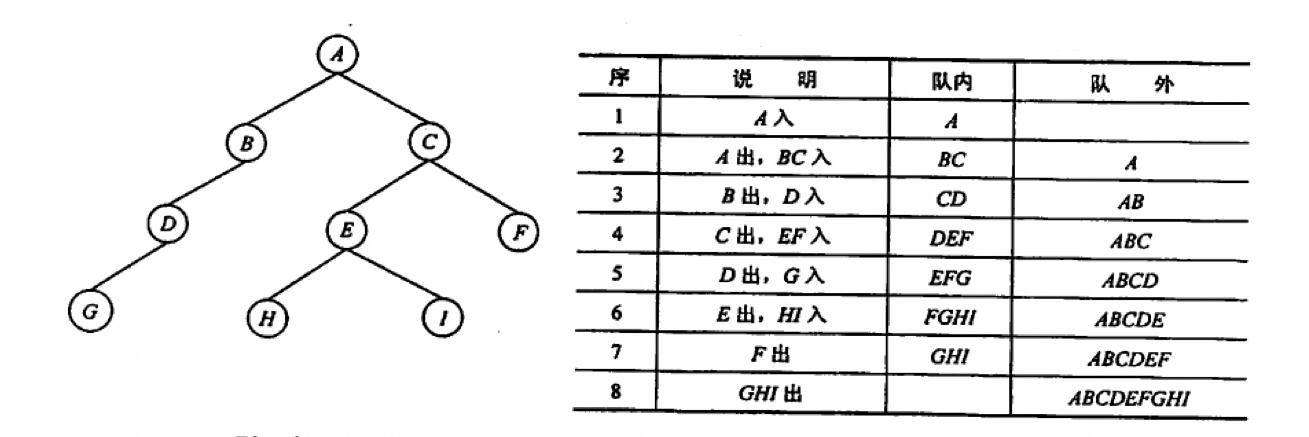
2.6.1. 层次遍历

对问题进行逐层或逐行处理。这类问题的解决方法往往在处理当前层或当前axing是就队下一层或下一行做预处理，把处理顺序安排好，等到当前层或当前行处理完毕，就可以处理下一层或下一行。使用队列是为了保存下一步的处理顺序。如二叉树的层次遍历，图的层次遍历。

层次遍历过程

跟结点入队；
若队空，则结束遍历；否则重复【3】操作；
队列中第一个结点出队，并访问之。若其有左孩子，则将左孩子入队；若其有有孩子，则将右孩子入队，返回【2】。

2.6.2. 在操作系统中的应用

在计算机系统中的作用：第一个方面是解决主机与外部设备之间速度不匹配的问题，第二个方面是解决有多用户引起的资源竞争问题。

多个进程争抢着使用有限的系统资源时，FCFS(First Come First Service，先来先服务)是一种常用策略。

Eg1：CPU资源的分配

Eg2：去学校打印店打印论文，多个同学用同一台打印机打印，打印的先后顺序如何?

3. 矩阵的压缩存储

3.1. 数组的存储结构

3.1.1. 一维数组

ElemType a[10];

	a[0]	a[1]	a[2]	a[3]	a[4]	a[5]	a[6]	a[7]	a[8]	a[9]

各数组元素大小相同，且物理上连续存放。

数组元素a[i] 的存放地址 = LOC + ixsizeof(ElemType) (0≤i<10)

3.1.2. 二维数组

ElemType b[2][4]; 2行4列的二维数组

逻辑视角

b[0] [0]	b[0] [1]	b[0] [2]	b[0] [3]
b[1] [0]	b[1] [1]	b[1] [2]	b[1] [3]

行优先存储

	b[0] [0]	b[0] [1]	b[0] [2]	b[0] [3]	b[1] [0]	b[1] [1]	b[1] [2]	b[1] [3]

M行N列的二维数组b[M] [N]中，若按行优先存储，则

b[i] [j]的存储地址=LOC+(ixN+j)xsizeof(ElemType)

列优先存储

	b[0] [0]	b[1] [0]	b[0] [1]	b[1] [1]	b[0] [2]	b[1] [2]	b[0] [3]	b[1] [3]

M行N列的二维数组b[M] [N]中，若按列优先存储，则

b[i] [j]的存储地址=LOC+(jxM+i )xsizeof(ElemType)

3.2. 特殊矩阵

压缩存储：为多个值相同的元素只分配一个存储空间，对零元素不分配存储空间。其目的是节省存储空间。

特殊矩阵：指具有许多相同矩阵元素或零元素，并且这些相同矩阵元素或零元素的分布有一定规律性的矩阵。常见的特殊矩阵有对称矩阵，上(下)三角矩阵，对角矩阵等。

3.2.1. 对称矩阵

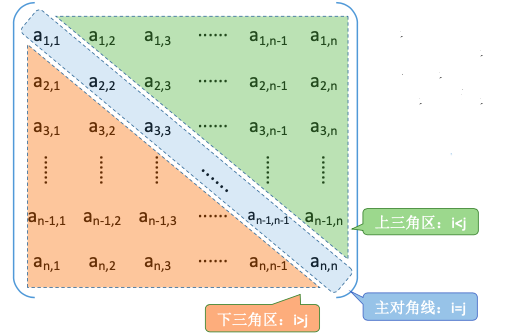
若 n 阶方阵中任意一个元素 a_i,j 都有 a_i,j = a_j,i 则该矩阵为对称矩阵

普通存储：n*n 二维数组

压缩存储策略：只存储主对角线+下三角区(或主对角线+上三角区)

策略:只存储主对角线+下三角区按行优先原则将各元素存入一维数组中。

B[0]	B[1]	B[2]	B[3]	…		B[$\frac{(1+n)n}{2}$-1]
a_1,1	a_2,1	a_2,2	a_3,1	…	a_n,n-1	a_n,n

思考:

数组大小应为多少?

$\frac{(1+n)*n}{2}$
站在程序员的角度，对称矩阵压缩存储后怎样才能方便使用?

可以实现一个“映射”函数

矩阵下标 -> 一维数组下标
按行优先的原则，a_i,j 是第几个元素?

[1+2+···+(i-1)] + j -> 第 $\frac{i(i-1)}{2}$ + j 个元素 -> k= $\frac{i(i-1)}{2}$+ j − 1
按行优先的原则，a_j,i是第几个元素?

ai,j = aj,i (对称矩阵性质)

k= $\frac{j(j-1)}{2}$ + 𝑖 − 1

故压缩到一维数组时，

下三角区和主对角线元素 k=$\frac{i(i-1)}{2}+j-1, i\geq j$，

上三角区元素a_i,j=a_j,i，k=$\frac{j(j-1)}{2}+i-1$, i<j

3.2.2. 三角矩阵

3.2.2.1. 下三角矩阵

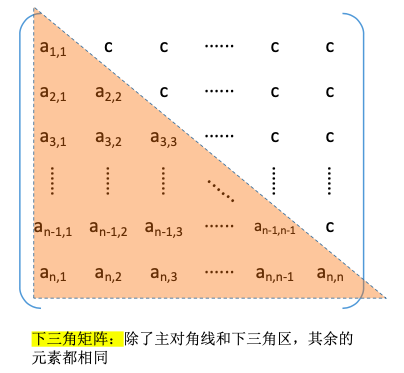
压缩存储策略：按行优先原则将橙色区元素存入一维数组中。并在最后一个位置存储常量c

B[0]	B[1]	B[2]	B[3]	…		B[$\frac{(1+n)n}{2}$-1]	B[$\frac{(1+n)n}{2}$]
a_1,1	a_2,1	a_2,2	a_3,1	…	a_n,n-1	a_n,n	C

按行优先的原则，a_i,j 是第几个元素?

下三角区和主对角线元素时，k=$\frac{i(i-1)}{2}+j-1, i\geq j$

上三角区元素时，k=$\frac{n(n+1)}{2}, i<j$

3.2.2.2. 上三角矩阵

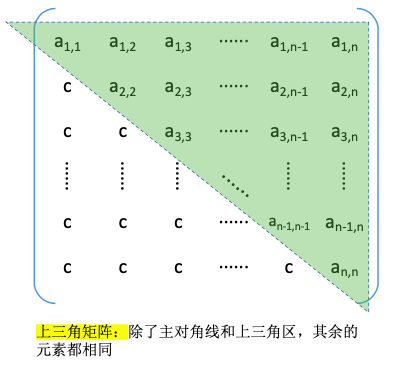
压缩存储策略：按行优先原则将绿色区元素存入一维数组中。并在最后一个位置存储常量c

B[0]	B[1]	B[2]	B[3]	…		B[$\frac{(1+n)n}{2}$-1]	B[$\frac{(1+n)n}{2}$]
a_1,1	a_1,2	a_1,3	a_1,4	…	a_n,n-1	a_n,n	C

按行优先的原则，ai,j 是第几个元素?

上三角区和主对角线元素，k= $\frac{(i-1)(2n-i+2)}{2}+(j-i), i\leq j$

下三角区元素，k=$\frac{n(n+1)}{2}, i>j$

3.2.3. 三对角矩阵

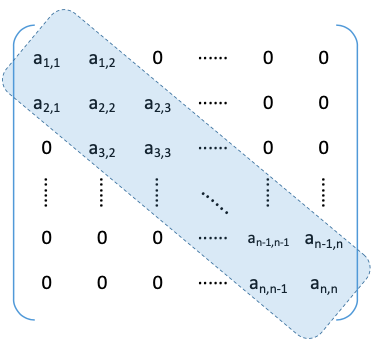
三对角矩阵，又称带状矩阵：当|i - j|>1时，有a$_{i,j}$ = 0 (1≤ i, j ≤n)

压缩存储策略：按行优先(或列优先)原则，只存储带状部分

B[0]	B[1]	B[2]	B[3]	…		B[3n-3]
a$_{1,1}$	a$_{1,2}$	a$_{2,1}$	a$_{2,2}$	…	a$_{n,n-1}$	a$_{n,n}$

a$_{i,j}$ (|i-j|$\leq$1) -> B[k]

按行优先的原则，a$_{i,j}$ 是第几个元素?

前i-1行共 3(i-1)-1 个元素

a$_{i,j}$是 i 行第 j-i+2 个元素

a$_{i,j}$是第 2i+j-2 个元素

数组下标从0开始：k = 2i+j-3
若已知数组下标k，如何得到 i, j ?

B[k] -> a$_{i,j}$

前i-1行共 3(i-1)-1 个元素，前i行共 3i-1 个元素，显然

3(i-1)-1 < k+1 ≤ 3i-1

i $\geq$ (k+2)/3

i = (k+2)/3 向上取整即可满足

王道书的计算逻辑：

3(i-1)-1 ≤ k < 3i-1
i $\leq$ (k+1)/3+1

i = (k+1)/3+1

j = k– 2i + 3

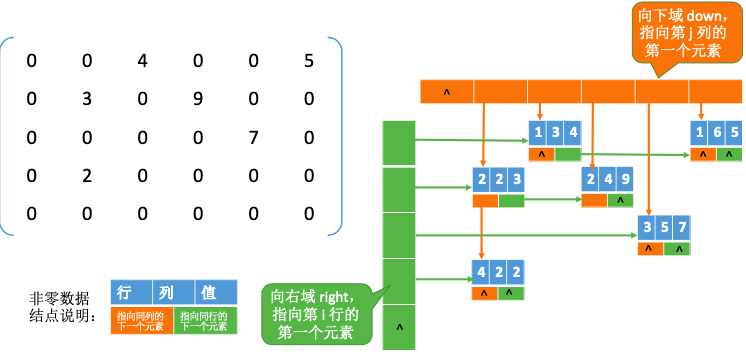
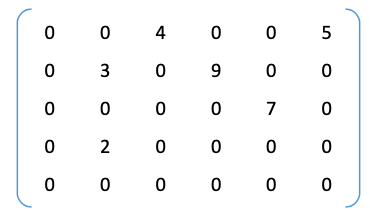
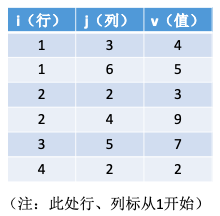
3.2.4. 稀疏矩阵

稀疏矩阵：非零元素远远少于矩阵元素的个数
压缩存储策略：顺序存储—三元组 <行，列，值>，链式存储——十字链表法