W.T.的博客

Every day to be a little better

算法笔记

置顶 发表于 更新于 分类于
本文字数： 40k 阅读时长 ≈ 36 分钟
算法笔记

1. 代码语言选择

java执行时间比较慢

c++语法向下兼容c

c++拥有STL标准模板库

2. 编译器

windows版：Dev-C++ – 浙大翁凯推荐

特点：轻便好用 – 新建文件，编写代码，保存后即可运行

mac版：Sublime Text

3. PAT

https://www.patest.cn/

浙大PAT。分为乙级，甲级，顶级。采用单点测试，处理一组数据的输入。

4. C/C++基础知识

4.1. 主函数main()

是一个程序的入口位置，整个程序从主函数开始执行

1
2
3
int main(){
  return 0;
}

4.2. scanf

读取数据

%d int型输入标识，&取得a所在地址

1
scanf("%d",&a);

常见数据类型变量的scanf格式符

数据类型 格式符 举例
int %d scanf(“%d”,&n);
long long %lld scanf(“%lld”,&n);
float %f scanf(“%f”,&n);
double %lf scanf(“%llf”,&n);
char %c scanf(“%c”,&n);
字符串 %s char str[12]; scanf(“%s”,str);

整型，浮点型以空格符为结束判断标志

字符串以空格/换行符为结束标志

字符可读入字符

字符数组以空格跟换行为读入结束的标志，另外数组名称本身就代表了这个数组第一个元素的地址。

4.3. prinf

输出数据，以%d int类型输出

1
printf("%d",a);

输出% 

1
printf("%%");

输出格式

格式 说明
%0md 以0补齐输出
%.mf 小数点为m位的浮点型
%md 以m位右对齐输出

4.4. cin/cout

1
2
3
4
5
6
7
8
9
#include<iostream>
using namespace std;
int main(){
  
  int n;
  cin>>n;
  cout<<n;
  return 0;
}

读入字符串

1
2
char str[100];
cin.getline(str,100);

or

1
2
string str;
getline(cin,str);

4.5. sscanf/sprintf

sscanf 将字符串转化为数字

sscanf(str,”%d”,&a) str以%d格式写到a中

1
2
3
4
5
6
#include <stdio.h>
int main(){
  char str[10]="123";
  int a=0;
  sscanf(str,"%d",&a);
}

sprintf

sprintf(str,”%d”,a); 把a以%d的格式写到str字符串中

1
2
3
4
5
6
#include <stdio.h>
int main(){
  int a =123;
  char str[10]; 
  sprintf(str,"%d",a);
}

4.6. getchar/putchar

char ch = getchar() 输入单个字符

puthar(ch) 输出ch字符

4.7. puts/gets

gets(string) 输入字符串，识别\n为结束

puts(string) 输出字符串

4.8. 变量类型

类型 取值范围 初值 scanf
整型 int -2x$10^{9}$ - 2x$10^{9}$ 0 %d
long long -9x$10^{18}$ - 9x$10^{18}$ 0LL %lld
浮点型 float -$2^{128}$ - $2^{128}$ 0.0f %f
double -$2^{1024}$ - $2^{1024}$ 0.0 %lf
字符 char -128 - 127 \0 %c
布尔 bool 0/1 %d

浮点数都用double

int 通常表示为 $2^{30}-1$ 以防两数相加超过int表示范围 即03ffffffH

字符常量char，在计算机内部用ASCII码0-127表示 。

显示字符 ASCII码
0-9 48-57
A-Z 65-90
a-z 97-122

4.8.1. 浮点数比较

相等

1
2
const double eps=1e-8;
#define Equ(a,b) (fabs((a)-(b))<(eps))

大于

1
#define More(a,b) (((a)-(b))>(eps))

小于

1
#define Less(a,b) (((a)-(b))<(-eps))

大于等于

1
#define MoreEqu(a,b) (((a)-(b))>(-eps))

小于等于

1
#define LessEqu(a,b) (((a)-(b))<(eps))

圆周率

1
const double pi=acos(-1.0);

4.8.2. 转义字符

\n 换行

\t 空格

\0 空字符null，ASCII码为0

4.8.3. 字符串常量

1
2
3
char str[25]="Hello World";
printf("%s",str);
scanf("%s",str);

字符数组名称本身代表数组第一个元素地址

以空格跟换行为读入结束标志

空字符\0在使用gets/scanf 时会自动添加在字符串最后

getchar() 不会在输入末尾加\0

4.8.4. 布尔型

c语言中必须加#include< stdbool.h>

整型常量在赋值给布尔型变量时会自动转换为true，1/-1都为true

if(n!=0) = if(n)

if(n==0) = if(!n)

4.8.5. 符号常量

一旦赋值，其值不再改变

  • 宏定义 #define pi 3.14

    宏定义直接将对应的部分替换，然后进行编译和运行

    必须加括号传输

    1
    #define CAL(a,b) ((a)+(b))

  • const double pi = 3.14；

4.9. typedef 起别名

1
2
typedef long long ll;
ll a = 123LL;

4.10. 数组

初始化

1
2
int a[10]={0};
int a[10]={};

数组大小大于$10^6$时，应定义在主函数外

赋相同值 memeset函数，只能赋-1/0（memset按字节赋值，对每个字节赋同样的值，组成int型的4个字节就会被赋成相同的值）

1
2
3
4
5
#include <string.h>
int main(){
  int a[5]={1,2,3,2,1};
  memset(a,0,sizeof(a));
}

数组为参数时，在函数中对数组元素的修改等同于对原数组元素的修改

4.11. 指针

每个变量都会存放在内存中分配的一个空间。每一个字节都会有一个地址。每个变量就是它占用的空间第一个字节的地址。

指针表示内存地址。C语言中用指针把地址指向一个变量。

指针本质是unsinged类型整数

1
2
3
4
5
6
7
8
9
int a = 2;
int* p = &a; //a的内存地址

*p=3; //p所指向的地址中存的是3，于是a的值也变为3
printf("%d",a); //3

//数组名称作为数组首地址使用
char str[10]="Hello";
int* q=str; //=&str[0];

指针与数组

1
2
int a[10]={0};
for(int* p=a; p<a+10; p++){}

4.12. 引用

引用操作的是原变量

1
2
3
4
5
6
7
8
9
void change(int &x){
  x=3;
}
int main(){
  int a = 2;
  change(a);
  printf("%d",a); //3
  return 0;
}

5. 头文件

5.1. stdio.h

标准输入输出库，standard input output，负责输入输出

1
#include <stdio.h>

5.2. math.h

数学函数

  • fabs(double) 绝对值函数
  • floor(double) 向下取整 4.5=4
  • ceil(double) 向上取整 4.5=5
  • round(double) 四舍五入取整 4.5=5; 4.4=4
  • pow(double a, double b) $a^b$
  • sqrt(double) 算术平方根
  • log(double) 以e为底的对数
  • sin(double), cos(double), tan(double)
  • asin(double), acos(double), atan(double)

5.3. string.h

  • strlen() 字符串长度
  • strcmp(string,string) 按字典顺序比较字符串 > = < 0
  • strcpy(string, string) 将字符串数组1复制给数组2
  • strcat(string, string) 字符数组2接到字符数组1后

6. 排序

6.1. 冒泡排序

交换数组元素。每次交换结果是将当前剩余元素的最大值移动到一端，剩余元素为0，排序成功

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
const int maxn=5;
int a[maxn]={3,2,1,5,4};

for(int i=0;i<=maxn-1;i++){ //4趟
  bool flag = true;
  //从前往后
  for(int j=0;j<maxn-1-i;j++){ //第一趟 0-4号元素
    if(a[j]>a[j+1]){ //将最大值移动至最后
      flag=false;
      int temp=a[j];
      a[j]=a[j+1];
      a[j+1]=temp;
    }
  }
  if(flag){ //说明当前元素排列已经有序
      return;
   }
}

way2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
for(int i=0;i<=maxn-1;i++){ //4趟
  bool flag = true;
  //从后往前
  for(int j=maxn-1;j>i;j--){ //第一趟 0-4号元素
    if(a[j-1]<a[j]){ //将最大值移动至最后
      flag=false;
      int temp=a[j-1];
      a[j]=a[j-1];
      a[j-1]=temp;
    }
  }
  if(flag){ //说明当前元素排列已经有序
      return;
   }
}

6.2. 简单选择排序

对一个序列A中的元素A[1]~A[n]，令i从1到n枚举，进行n趟操作。每趟从待排序部分[i,n]中挑选最小的元素，令其与待排序部分的第一个元素A[i]进行交换。这样A[i]就会与当前有序区间[1,i-1]形成新的有序区间[1,i]。n趟后，所有元素就是有序的。

1
2
3
4
5
6
7
8
9
10
11
12
13
for(int i=0;i<n-1;i++){
  int min=i;
  for(int j=i+1;j<n;j++){
    if(a[j]<a[min]){
      min=j;
    }
  }
  if(min!=i){
    int temp=a[min];
    a[min]=a[i];
    a[i]=temp;
  }
}

6.3. 插入排序

将序列A分成有序区间A[0,i-1]和无序区间A[i,n-1]，将A[i]插入到有序区间中形成新的有序区间。n-1趟后序列有序

1
2
3
4
5
6
7
8
9
10
for(int i=1;i<n;i++){
  if(a[i]<a[i-1]){
    int temp=a[i];
    int j=i-1;
    for(;a[j]>temp&&j>=0;j--){
      a[j+1]=a[j];
    }
    a[j+1]=temp;
  }
}

6.4. 归并排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
int temp[110]={};
void merge(int a[],int l1,int r1,int l2,int r2){
  int index=0;
  int i=l1; int j=l2;
  while(i<=r1&&j<=r2){
    if(a[i]<=a[j]){
      temp[index++]=a[i++];
    }else{
      temp[index++]=a[j++];
    }
  }
  while(i<=r1){
    temp[index++]=a[i++];
  }
  while(j<=r2){
    temp[index++]=a[j++];
  }
  for(int i=0;i<index;i++){
    a[l1+i]=temp[i];
  }
}

6.4.1. 递归

1
2
3
4
5
6
void mergeSort(int a[],int left,int right){
  int mid=(left+right)/2;
  mergeSort(a,left,mid);
  mergeSort(a,mid+1,right);
  merge(a,left,mid,mid+1,right);
}

6.4.2. 非递归

1
2
3
4
5
6
7
8
9
10
11
12
void mergeSort(int a[]){
  //step 组内元素个数
  for(int step=2;step/2<=n;step*=2){
    //每组step个元素，前step/2和后step/2合并
    for(int i=1;i<=n;i+=step){
      int mid=i+step/2-1;
      if(mid+1<=n){
        merge(a,i,mid,mid+1,min(i+step-1,n));
      }
    }
  }
}

6.4.3. sort

1
2
3
4
5
6
7
void mergeSort(int a[]){
  for(int step=2;step/2<=n;step*=2){
    for(int i=1;i<=n;i+=step){
      sort(a+i,a+min(i+step,n+1));
    }
  }
}

6.5. 快排

挑选a[0]为中枢值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int Partition(int a[],int left,int right){
  int temp=a[left];
  while(left<right){
    while(left<right&&a[right]>temp){
      right--;
    }
    a[left]=a[right];
    while(lefth<right&&a[left]<temp]){
      left++;
    }
    a[right]=a[left];
  }
  a[left]=temp;
  return left;
}
void quickSort(int a[],int left,int right){
  int mid=Partition(a,left,right);
  quickSort(a,left,mid-1);
  quickSort(a,mid+1,right);
}

随机数，将生成[left,right]内的随机数对应的数组元素作为中枢值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include<stdlib.h>
#include<time.h>
#include<stdio.h>
int Partition(int a[],int left,int right){
  srand((unsigned)time(NULL));
  int p=(int)(round(1.0*rand()/RAND_MAX*(right-left)+left));
  swap(a[p],a[left]);
  
  int temp=a[left];
  while(left<right){
    while(left<right&&a[right]>temp){
      right--;
    }
    a[left]=a[right];
    while(lefth<right&&a[left]<temp]){
      left++;
    }
    a[right]=a[left];
  }
  a[left]=temp;
  return left;
}

6.5.1. 求第K大的值

1
2
3
4
5
6
7
8
9
10
11
12
void findK(int a[],int left,int right,int k){
  if(a[left]==a[right])
    return a[left];
  int p=Partition(a,left,right);
  int m=p-left+1;
  if(k==m)
    return a[p];
  else if(k<m)
    findK(a,left,p-1,k);
  else
    findK(a,p+1,right,k-m);
}

6.6. 排名的实现

1
2
3
4
5
6
7
8
stu[0].rank=1;
for(int i=1;i<n;i++){
  if(stu[i].score==stu[i-1].score){
    stu[i].rank=stu[i-1].rank;
  }else{
    stu[i].rank=i+1;
  }
}

直接打印

1
2
3
4
5
6
7
int r=1;
for(int i=0;i<n;i++){
  if(i!=0&&stu[i].score!=stu[i-1].score){
    r=i+1;
  }
  printf("%d",r);
}

6.7. 堆排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
void downAdjust(int low,int high){
  int i=low; int j=i*2;
  while(j<=high){
    if(j+1<=high&&heap[j+1]>heap[j]){
      j++;
    }
    if(heap[j]>heap[i]){
      swap(heap[i],heap[j]);
      i=j;
      j=i*2;
    }else{
      break;
    }
  }
}

void createHeap(int x){
  for(int i=n/2;i>=1;i--){
    downAdjust(i,n);
  }
}

void deleteTop(){
  heap[1]=heap[n--];
  downAdjust(1,n);
}

void updateAdjust(int low,int high){
  int i=high; int j=i/2;
  while(j>=low){
    if(heap[j]<heap[i]){
      swap(heap[j],heap[i]);
      i=j;
      j=i/2;
    }else{
      break;
    }
  }
}

void insert(int x){
  heap[++n]=x;
  updateAdjust(1,n);
}


void heapSort(){
  createHeap();
  for(int i=n;i>1;i--){
    swap(heap[1],heap[i]);
    downAdjust(1,i-1);
  }
}

7. 散列

7.1. 散列函数

H(key)=key%mod;

mod 取不小于表长的最小素数

  • Linear Probing线性探测：寻找H(key)+1位置是否被占据
  • Quadratic Probing 平方探查法：H(key)+/-$k^2$ 位置
  • 链地址法：H(key) 串在同一个位置后

7.2. 字符串转整数

1
2
3
4
int ans=0;
for(int i=0;ch[i]!='\0';i++){
  ans=ans*26+ch[i]-'0';
}

8. 分治

分而治之。

分解原问题，解决子问题，合并解。

8.1. 递归

  • 递归边界
  • 递归式

8.1.1. 全排列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include<cstdio>
const int maxn=11;
int n=3;
int p[maxn]={};
int hashTable[maxn]={};
void generateP(int index){
  //说明已经排好
	if(index==n+1){
		for(int i=1;i<=n;i++){
			printf("%d", p[i]);
		}
		printf("\n");
		return;
	}
	for (int x = 1; x <=n ; ++x)
	{
		if (hashTable[x]==0)
		{
			p[index]=x;
			hashTable[x]++;
			generateP(index+1);
			hashTable[x]--;//还原状态
		}
	}

}
int main(){
	generateP(1);
	return 0;
}

8.1.2. n皇后

每个皇后都不在同一行，同一列，同一条对角线上。

采用全排列的方法。固定列，行号为排列号。故比较排列号即可得知n皇后是否成立。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include<cstdio>
const int maxn=11;
int n=3;
int p[maxn]={};
int hashTable[maxn]={};
int cnt=0;
void generateP(int index){
	if(index==n+1){
		cnt++;
		return;
	}
	for (int x = 1; x <=n ; ++x)
	{
		if (hashTable[x]==0)
		{
      bool flag=true;
      
      for(int pre=1;pre<index;pre++){
        if(abs(pre-index)==abs(p[pre]-x)){
          //前面已经不能组成n皇后，没必要继续排列
          flag=false;
          break;
        }
      }
      if(flag){
          p[index]=x;
          hashTable[x]++;
          generateP(index+1);
          hashTable[x]--;
      }
		}
	}

}
int main(){
	generateP(1);
	return 0;
}

9. 贪心

局部最优策略。

B1020 月饼 – 选择单价最高的

B1023 组个最小数

9.1. 区间贪心

9.1.1. 区间不相交的最多开区间

总是选择左端点最大的区间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=110;
struct node{
  int x,y;
}I[maxn];
bool cmp(node a,node b){
  if(a.x!=b.x){
    return a.x>b.x;
  }else{
    return a.y<b.y;
  }
}
int main(){
  int n;
  scanf("%d",&n);
  for(int i=0;i<n;i++){
    scanf("%d%d",&I[i].x,I[i].y);
  }
  sort(I,I+n,cmp);
  int ans=1;
  int lastX=I[0].x;
  for(int i=1;i<n;i++){
    if(I[i].y<=lastX){
      lastX=I[i].x;
      ans++;
    }
  }
  printf("%d",ans);
  return 0;
}

9.1.2. 最少点数使每个区间都至少存在一个点

取左端点就能尽可能覆盖其他区间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=110;
struct node{
  int x,y;
}I[maxn];
bool cmp(node a,node b){
  if(a.x!=b.x){
    return a.x>b.x;
  }else{
    return a.y<b.y;
  }
}
int main(){
  int n;
  scanf("%d",&n);
  for(int i=0;i<n;i++){
    scanf("%d%d",&I[i].x,I[i].y);
  }
  sort(I,I+n,cmp);
  int ans=1;
  int lastX=I[0].x;
  for(int i=1;i<n;i++){
    if(I[i].y<lastX){
      lastX=I[i].x;
      ans++;
    }
  }
  printf("%d",ans);
  return 0;
}

10. 二分

10.1. 二分查找

left<=right ，当left>right时不再是闭区间，作为元素不存在的判定原则。

1
2
3
4
5
6
7
8
9
10
11
12
13
int binarySearch(int a[],int left,int right,int x){
  while(left<=right){
    int mid=(left+mid)/2;
    if(a[mid]==x)
      return;
    else if(a[mid]>x){
      right=mid-1;
    }else{
      left=mid+1;
    }
  }
  return -1;
}

10.2. 第一个>=x的位置

区间是左闭右开的，left<right，当left==right时，夹出的是唯一的位置，返回的是left/right

1
2
3
4
5
6
7
8
9
10
11
12
13
int lower_bound(int a[],int left,int right,int x){
  while(left<right){
    int mid=(left+mid)/2;
    if(a[mid]==x)
      return;
    else if(a[mid]>=x){
      right=mid;
    }else{
      left=mid+1;
    }
  }
  return left;
}

10.3. 第一个大于x的位置

1
2
3
4
5
6
7
8
9
10
11
12
13
int uppper_bound(int a[],int left,int right,int x){
  while(left<right){
    int mid=(left+mid)/2;
    if(a[mid]==x)
      return;
    else if(a[mid]>x){
      right=mid;
    }else{
      left=mid+1;
    }
  }
  return left;
}

10.4. 求根值近似值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
const double eps=1e-5;
double f(double x){
  return x*x;
}
int calSqrt(){
  int left=1;
  int right=2;
  while(right-left<eps){
    int mid=(left+mid)/2;
    if(f(mid)>2)
      right=mid;
    else{
      left=mid;
    }
  }
  return mid;
}

11. 快速幂

$a^b$%m

1
2
3
4
5
6
7
8
9
10
typedef long long ll;
ll binaryPow(ll a,ll b,ll m){
  ll ans=1LL;
  if(b&1){ //b的二进制末尾是否为1
    ans=ans*a%m;
  }
  a=a*a%m;
  b=b>>1;
  return ans;
}

12. two points

12.1. a[i]+a[j]=m

1
2
3
4
5
6
7
8
9
10
11
12
int i=0;
int j=n-1;
while(i<j){
  if(a[i]+a[j]==m){
    i++;
    j--;
  }else if(a[i]+a[j]<m){
    i++;
  }else{
    j--;
  }
}

13. 数学问题

13.1. 最大公约数

1
2
3
4
5
6
int gcd(int a,int b){
  if(b==0)
    return a;
  else
    return gcd(b,a%b);
}

法二：

如：12，20

最大公约数从1，2，3，… ，12中产生，故从两数中的较小者开始计算

1
2
3
4
5
6
7
8
9
int gcd(int a,int b){
  int min = (a<b)?a:b;
  for(int i = min ;i>=1;i--){
    if(a%i==0 && b%i==0){
      return i;
    }
  }
  return -1;
}

13.2. 最小公倍数

1
2
3
4
int lcm(int a,int b){
  int d=gcd(a,b);
  return a/d*b;
}

法二：

1
2
3
4
5
6
7
8
9
int lcm(int a,int b){
  int max = (a>b)?a:b;
  for(int i = max ;i<= a*b;i++){
    if(i%a==0 && i%b==0){
      return i;
    }
  }
  return -1;
}

13.3. 分数四则运算

13.3.1. 初始化

1
2
3
struct fraction{
  int up,down;
};

13.3.2. 化简

1
2
3
4
5
6
7
8
9
10
11
12
13
14
fraction reduction(fraction result){
  if(result.down<0){
    result.down=-result.down;
    result.up=-result.up;
  }
  if(result.up==0){
    result.down=1;
  }else{
    int d=gcd(abs(result.up),abs(result.down));
    result.up/=d;
    result.down/=d;
  }
  return result;
}

13.3.3. 加

1
2
3
4
5
6
fraction add(fraction a,fraction b){
  fraction result;
  result.up=a.up*b.down+a.down*b.up;
  result.down=a.down*b.down;
  return reduction(result);
}

13.3.4. 减

1
2
3
4
5
6
fraction minu(fraction a,fraction b){
  fraction result;
  result.up=a.up*b.down-a.down*b.up;
  result.down=a.down*b.down;
  return reduction(result);
}

13.3.5. 乘

1
2
3
4
5
6
fraction multi(fraction a,fraction b){
  fraction result;
  result.up=a.up*b.up;
  result.down=a.down*b.down;
  return reduction(result);
}

13.3.6. 除

1
2
3
4
5
6
fraction divide(fraction a,fraction b){
  fraction result;
  result.up=a.up*b.down;
  result.down=a.down*b.up;
  return reduction(result);
}

13.3.7. 输出

1
2
3
4
5
6
7
8
9
10
void showResult(fraction result){
  result=reduction(result);
  if(result.down==1){
    printf("%d",result.up);
  }else if(abs(result.up)>result.down){
    printf("%d %d/%d",result.up/result.down),abd(result.up)%result.down,result.down);
  } else{
    printf("%d/%d",result.up,result,down);
  }
}

13.4. 大数运算

高位存储在数组的高位，低位存储在数组的低位。

13.4.1. 表示

字符串是从高位开始存储的

1
2
3
4
5
6
char ch[maxn];
int len=strlen(ch);
int num[maxn]={};
for(int i=0;i<len;i++){
  num[i]=ch[len-1-i]-'0';
}

13.4.2. 比较两个大数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int compare(int a[],int b[]){
  if(lena>lenb) //a比b长说明a更大
    return 1;
  else if(lena<lenb)
    return -1;
  else{
    //从高位开始逐个比较
    for(int i=lena-1;i>=0;i--){
      if(a[i]>b[i])
        return 1;
      else if(a[i]<b[i])
        return -1;
    }
    return 0;
  }
  
}

13.4.3. 高精度加

1
2
3
4
5
6
7
8
9
10
11
12
void add(int a[],int b[],int ans[]){
  int carry=0;
  int index=0;
  for(int i=0;i<lena||i<lenb;i++){
    int temp=a[i]+b[i]+carry;
    ans[index++]=temp%10;
    carry=temp/10;
  }
  if(carry!=0){
    ans[index++]=carry;
  }
}

13.4.4. 高精度减

1
2
3
4
5
6
7
8
9
10
11
12
13
void sub(int a[],int b[],int ans[]){
  int index=0;
  for(int i=0;i<lena||i<lenb;i++){
    if(a[i]<b[i]){
      a[i++]--;
      a[i]+=10;
    }
    ans[index++]=a[i]-b[i];
  }
  while(ans[index-1]==0&&index-1>=1){
    index--;
  }
}

13.4.5. 乘

1
2
3
4
5
6
7
8
9
10
11
12
13
void mutl(int a[],int b,int ans[]){
  int carry=0;
  int index=0;
  for(int i=0;i<lena;i++){
    int temp=a[i]*b+carry;
    ans[index++]=temp%10;
    carry=temp/10;
  }
  while(carry!=0){
    ans[index++]=carry%10;
    carry/=10;
  }
}

13.4.6. 除

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void divide(int a[],int b,int ans[]){
  int r=0;
  int index=0;
  for(int i=lena-1;i>=0;i--){
    int r=r*10+a[i];
    if(r<b){
      ans[i]=0;
    }else{
      ans[i]=r/b;
      r=r%b;
    }
  }
  while(ans[index-1]==0&&index-1>=1){
    index--;
  }
}

14. c++标准模版库

14.1. vector

1
2
#include<vector>
using namespace std;

变长数组 vector< typename> v; = typename v[maxn];

访问

  • v[i]

  • for(vector<int>::iterator it=v.begin();it!=v.end();it++){
  printf("%d",*it);
}

    1
    2
    3
    4
    5
    6
    7

    v.end() 取的是vector末尾下一个地址

    添加元素**

    ```c++
    v.push_back(); //添加到尾部

删除元素

删除尾部元素

1
v.pop_back();

个数

1
v.size(); //unsigned

插入

1
v.insert(v.begin()+2,-1); //-1插入到v[2]

删除

1
2
3
v.erase(v.begin()+2); //删除v[2]
//[first,second)
v.erase(v.begin(),v.begin()+3); //删除v[0],v[1],v[2]

14.2. set

内部自动升序且不含重复元素的容器。

1
2
3
4
5
6
7
8
9
10
11
12
set<typename> s;
//插入
s.insert();
//遍历
for(set<typename>::iterator it=s.begin();it!=s.end();it++){
  *it
}
//查询
*(s.find(2));
//删除
s.erase(s.find(2));
s.erase(s.find(2),s.end());

14.3. string

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<string>
using namespace std;
string str="...";
//string -> char[]
char[] =str.c_str();
//char[] -> string
char ch[]=str;

//直接比较字典序
str1 < str2;

//str[1]处插入“123”
str.insert(1,"123");
str.insert(str.begin()+1,str1.begin(),str.end());

//删除
str.erase(str.begin());
str.erase(str.begin(),str.end());
str.erase(3,2);//删除3号位开始的2个字符

//清空
str.clear();

//子串
str.substr(0,3); //0号位开始长度为3的子串

//失配
string::npos = -1;
  
//查找
str.find(".."); //返回第一次出现的位置

//替换
str.replace(10,4,str2); //10号位开始，长度为4的子串替换为str2
//[0,2)范围子串替换为str2
str.replace(str.begin(),str.begin()+2,str2);

14.4. map

以键从小到大顺序自动排序，内部为红黑树结构

1
2
3
4
5
6
7
8
9
10
11
12
13
#include<map>
using namespace std;
map<int,int> m;

//访问
m[0]=1;
map<int,int>::iterator it=m.begin();
it->first;
it->second;

//find(0)

//erase

14.5. queue

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include<queue>
using namespace std;

queue<int> q;
//压入队尾
q.push(0);
//推出队头
q.pop();

//队头元素
q.front();
//队尾元素
q.back();

//判空
q.empty();

//尺寸
q.size();

14.6. priority_queue

优先队列，堆结构。队头是优先级最高的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<priority_queue>
using namespae std;
priority_queue<int> q;
//入队
q.push(1);

//出队
q.pop();

//队头
q.top();

//判空
q.empty();

//个数
q.size();

//自定义优先级
//vector<int>承接底层堆的容器
//less<int>数字大优先级越高
//greater<int>数字大优先级越低
priority_queue<int,vector<int>,less<int>> q;

struct node{
  int price;
  friend bool operator < (const node &a,const node &b){
    return a.price<b.price;
  }
};
//按价格高排序
priority_queue<node> p;

14.7. stack

1
2
3
4
5
6
7
8
9
10
#include<stack>
using namespace std;

stack<int> s;

s.push(1);
s.pop();
s.top();
s.empty();
s.size();

14.8. pair

1
2
3
4
5
6
7
8
9
10
#include<utility>
using namespace std;
//初始化
pair<int,int> p(1,1);
p=pair<int,int>(1,1);
p=make_pair(1,1);

//取值
p.first;
p.second;

14.9. alogirthm

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include<alogrithm>
using namespace std;

//比大小
max(x,y);
min(x,y);

//绝对值,x为int，浮点数用fabs,在math库中
abs(x);

//交换值
swap(x,y);

//置换数组
reverse(a,a+4);

//全排列的下一个序列
next_permutation(a,a+3);

//赋予数组同一个值
fill(a,a+4,0);

//排序
sort(a,a+4); //升序
sort(a,a+4,cmp);//条件排序

//[first,last)内第一个>=val元素的位置/指针
lower_bound(first,last,val);
//[first,last)内第一个>val元素的位置/指针
upper_bound(first,second,val);

15. 数据结构

15.1. 栈

后进先出数据结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
void clear(){
  top=-1;
}

int size(){
  return top+1;
}

bool empty(){
  if(top==-1)
    return true;
  else
    return false;
}

void push(int x){
  s[++top]=x;
}

void pop{
  top--;
}

int top(){
  return s[top];
}

15.1.1. 算式运算

（ */ / +/- ）
栈内 1 5 3 6
栈外 6 4 2 1

栈内>=栈外时退栈

15.2. 队列

前进前出数据结构

front指向队首前一个位置，rear指向队尾位置

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void clear(){
  front=rear=-1;
}

int size(){
  return rear-front;
}

void push(int x){
  q[++rear]=x;
}

void pop(){
  front++;
}

int getFront(){
  return q[front+1];
}

15.3. 链表

15.3.1. 动态链表

1
2
3
4
5
6
7
8
9
10
11
12
struct node{
  int data;
  node* next;
};

//c
node* p=(node*)malloc(sizeof(node));
free(p);

//c++
node* p=new node;
delete(p);

15.3.2. 静态链表

1
2
3
struct node{
  int data,next;
}list[maxn];

15.4. 树

15.4.1. 二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
struct node{
  int data;
  node *lchild,*rchild;
};

node* newNode(int x){
  node* nownode=new node;
  nownode->data=x;
  nownode->lchild=nownode->rchild=NULL;
  return nownode;
}

//查找
node* search(node* root,int x){
  if(root==NULL){
    return NULL;
  }
  if(root->data==x){
    return root;
  }
  search(root->lchild,x);
  search(root->rchild,x);
}

//插入
void insert(node* &root,int x){
  if(root==NULL){
    root=newNode(x);
    return;
  }
  if( ){
    insert(root->lchild,x);
  }else{
    insert(root->rchild,x);
  }
}

//前序遍历 左根右
void preorder(node* root){
  if(root==NULL)
    return;
  printf("%d",root->data);
  preorder(root->lchild);
  preorder(root->rchild);
}

15.4.2. 前+中=树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
node* create(int prel,int prer,int inl,int inr){
  if(prel>prer)
    return NULL;
  node* root=new node;
  root->data=pre[prel];
  
  int i=inl;
  for(;i<=inr;i++){
    if(pre[prel]==in[i])
      break;
  }
  
  int numLeft=i-inl;
  root->lchild=create(prel+1,prel+numLeft,inl,i-1);
  root->rchild=create(prel+numLeft+1,prer,i+1,inr);
  return root;
}

15.4.3. 后+中=树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
node* create(int postl,int postr,int inl,int inr){
  if(postl>postr)
    return NULL;
  node* root=new node;
  root->data=post[postr];
  int i=inl;
  for(;i<=inr;i++){
    if(post[postr]==in[i])
      break;
  }
  int numLeft=i-inl;
  root->lchild=create(postl,postl+numLeft-1,inl,i-1);
  root->rchild=create(postl+numLeft,postr-1,i+1,inr);
  return root;
}

15.4.4. BST 二叉查找树

左子树<= 根<右子树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
//删除结点
node* findMax(node* root){
  while(root->rchild!=NULL){
    root=root->rchild;
  }
  return root;
}

node* findMin(node* root){
  while(root->lchild!=NULL){
    root=root->lchild;
  }
  return root;
}

void deleteNode(node* &root,int x){
  if(root==NULL)
    return;
  if(root->data==x){
    if(root->lchild==NULL&&root->rchild==NULL)
      root=NULL;
    else if(root->lchild!=NULL){
      node* maxNode=findMax(root->lchild);
      root->data=maxNode->data;
      deleteNode(root->lchild,maxNode->data);
    }else{
      node* minNode=findMin(root->rchild);
      root->data=minNode->data;
      deleteNode(root->rchild,minNode->data);
    }
  }else if(root->data>x){
    deleteNode(root->lchild,x);
  }else{
    deleteNode(root->rchild,x);
  }
}

15.4.5. AVL平衡二叉树

左子树和右子树的高度之差绝对值不超过1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
struct node{
  int data,height;
  node *lchild,*rchild;
}

node* newNode(int x){
  node* root=new node;
  root->data=x;
  root->height=1;
  root->lchild=root->rchild=NULL;
  return root;
}

int getHeight(node* root){
  if(root==NULL)
    return 0;
  else{
    return root->height;
  }
}

int getBalanceFactor(node* root){
  return getHeight(root->lchild)-getHeight(root->rchild);
}
void updateHeight(node* root){
  root->height=max(getHeight(root->lchild),getHeight(root->rchild))+1;
}

void L(node* &root){
  node* temp=root->rchild;
  root->rchild=temp->lchild;
  temp->lchild=root;
  updateHeight(root);
  updateHeight(temp);
  root=temp;
}

void R(node* &root){
  node* temp=root->lchild;
  root->lchild=temp->rchild;
  temp->rchild=root;
  updateHeight(root);
  updateHeight(temp);
  root=temp;
}

void insert(node* &root,int x){
  if(root==NULL){
    root=newNode(x);
    return;
  }
  if(root->data>x){
    insert(root->lchild,x);
    updateHeight(root);
    if(getBalanceFactor(root)==2){
      if(getBalanceFactor(root->lchild)==1){
        R(root);
      }
      if(getBalanceFactor(root->lchild)==-1){
        L(root->lchild);
        R(root);
      }
    }
  }else{
    insert(root->rchild,x);
    updateHeight(root);
    if(getBalanceFactor(root)==2){
      if(getBalanceFactor(root->rchild)==1){
        L(root);
      }
      if(getBalanceFactor(root->rchild)==-1){
        R(root->rchild);
        L(root);
      }
    }
  }
}

15.4.6. 并查集

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
//初始时每个元素独立
for(int i=0;i<n;i++){
  father[i]=i;
}

int findFather(int x){
  int a=x;
  while(x!=father[x]){
    x=father[x];
  }
  while(a!=father[a]){
    int z=a;
    a=father[a];
    father[z]=x;
  }
  return x;
}

void union(int x,int y){
  int fathera=findfather(x);
  int fatherb=findfather(y);
  if(fathera!=fatherb){
    father[fathera]=fatherb;
  }
}

15.4.7. 堆

完全二叉树，[1,n]记录结点

15.5. 图

15.5.1. dfs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
bool visit[maxn]={false};
void dfs(int u,int depth){
  visit[u]=true;
  for(int v=0;v<n;v++){
    if(visit[v]==false&&graph[u][v]!=inf){
      dfs(v,depth+1);
    }
  }
}
void dfsTrave(){
  for(int u=0;u<n;u++){
    if(visit[u]==false){
      dfs(u,1);
    }
  }
}

15.5.2. bfs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
bool visit[maxn]={false};
void bfs(int u){
  queue<int> q;
  q.push(u);
  visit[u]=true;
  while(!q.empty()){
    int top=q.front();
    q.pop();
    for(int i=0;i<graph[u].size();i++){
      int v=graph[u][i];
      if(visit[v]==false){
        q.push(v);
        visit[v]=true;
      }
    }
  }
}

void bfsTrave(){
  for(int u=0;u<n;u++){
    if(visit[u]==false){
      bfs(u);
    }
  }
}

15.5.3. 最短路径

15.5.3.1. Dijkstra

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=1000;
const int inf=0x03ffffff;
bool visit[maxn]={false};
int graph[maxn][maxn];
int d[maxn];
void dijkstra(int s){
  d[s]=0;
  for(int i=0;i<n;i++){
    int u=-1; int min=inf;
    for(int j=0;j<n;j++){
      if(visit[j]==false&&d[j]<min){
        min=d[j];
        u=j;
      }
    }
    if(u==-1){
      return;
    }
    visit[u]=true;
    for(int v=0;v<n;v++){
      if(visit[v]==false&&graph[u][v]!=inf){
        if(d[v]>d[u]+graph[u][v]){
          d[v]=d[u]+graph[u][v];
        }
      }
    }
  }
}
int main(){
  fill(d,d+maxn,inf);
  fill(graph[0],graph[0]+maxn*maxn,inf);
  
  return 0;
}
15.5.3.1.1. 求最短路径编号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
d[s]=0;
pre[s]=s;
if(visit[v]==false&&graph[u][v]!=inf){
    if(d[v]>d[u]+graph[u][v]){
      d[v]=d[u]+graph[u][v];
      pre[v]=u;
    }
  }

void dfs(int s,int v){
  if(v==s){
    printf("%d",s);
  }
  dfs(s,pre[v]);
  printf("%d",v);
}

vector<int> tempPath,path;
int minCost=0x3ffffff;
void dfs(int v){ 
  if(v==s){
    tempPath.push_back(v);
    int tempCost=0;
    for(int i=tempPath.size()-1;i>=0;i--){
      int id=tempPath[i];
      int nextId=tempPath[i-1];
      tempCost+=cost[id][nextId];
    }
    if(tempCost<minCost){
      minCost=tempCost;
      path=tempPath;
    }
    tempPath.pop_back();
    return;
  }
  tempPath.push_back(v);
  for(int i=0;i<pre[v].size();i++){
    dfs(pre[v][i]);
  }
  tempPath.pop_back(); 
}

15.5.3.1.2. 边权
1
2
3
4
5
6
7
8
9
c[s]=0;
if(visit[v]==false&&graph[u][v]!=inf){
  if(d[v]>d[u]+graph[u][v]){
    d[v]=d[u]+graph[u][v];
    c[v]=c[u]+cost[u][v];
  }else if(d[v]==d[u]+graph[u][v]&&c[v]>c[u]+cost[u][v]){
    c[v]=c[u]+cost[u][v];
  }
}
15.5.3.1.3. 点权
1
2
3
4
5
6
7
8
9
w[s]=weight[s];
if(visit[v]==false&&graph[u][v]!=inf){
  if(d[v]>d[u]+graph[u][v]){
    d[v]=d[u]+graph[u][v];
    w[v]=w[u]+weight[v];
  }else if(d[v]==d[u]+graph[u][v]&&w[v]<w[u]+weight[v]){
    w[v]=w[u]+weight[v];
  }
}
15.5.3.1.4. 最短路径条数
1
2
3
4
5
6
7
8
9
num[s]=1;
if(visit[v]==false&&graph[u][v]!=inf){
  if(d[v]>d[u]+graph[u][v]){
    d[v]=d[u]+graph[u][v];
    num[v]=num[u];
  }else if(d[v]==d[u]+graph[u][v]){
    num[v]+=num[u];
  }
}

15.5.3.2. Bellman-Ford

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
struct node{
  int v,dis;
  node(int _v,int _dis): v(_v),dis(_dis){}
};
vector<node> adj[maxn];
int d[maxn];

bool Bellman(int s){
  fill(d,d+maxn,inf);
  d[s]=0;
  for(int i=0;i<n-1;i++){ //n-1趟
    for(int u=0;u<n;u++){ //遍历所有边
      for(int j=0;j<adj[u].size();j++){
        int v=adj[u][j].v;
        int dis=adj[u][j].dis;
        if(d[u]+dis<d[v]){
          d[v]=d[u]+dis;
        }
      }
    }
  }
  
  for(int u=0;u<n;u++){
    for(int j=0;j<adj[u].size();j++){
        int v=adj[u][j].v;
        int dis=adj[u][j].dis;
        if(d[u]+dis<d[v]){
         return false; //存在负环
        }
      }
  }
  return true;
}
15.5.3.2.1. 求最短路径
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include<cstdio>
#include<algorithm>
#include<set>
#include<vector>
using namespace std;
struct node{
  int v,dis;
  node(int _v,int _dis): v(_v),dis(_dis){}
}
const int maxn=1000;
const int inf=0x3ffffff;
int num[maxn]={};
int d[maxn]={};
int w[maxn]={};
int weight[maxn]={};
vector<node> adj[maxn];
set<int> pre[maxn];

void Bellman(int s){
  fill(d,d+maxn,inf);
  d[s]=0;
  w[s]=weight[s];
  num[s]=1;
  for(int i=0;i<n-1;i++){
    for(int u=0;u<n;u++){
      for(int j=0;j<adj[u].size();j++){
        int v=adj[u][j].v;
        int dis=adj[u][j].dis;
        
        if(d[v]>d[u]+dis){
          
          d[v]=d[u]+dis;
          w[v]=w[u]+weight[v];
          num[v]=num[u];
          pre[v].clear();
          pre[v].insert(u);
          
        }else if(d[v]==d[u]+dis){
          if(w[u]+weight[v]>w[v]){
            w[v]=w[u]+weight[v];
          }
          pre[v].insert(u);
          num[v]=0;
          set<int>::iterator it;
          for(it=pre[v].begin();i!=pre[v].end();i++){
            num[v]+=num[*it];
          }
        }
      }
    }
  }
}

15.5.3.3. SPFA

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include<cstdio>
#include<algorithm>
#include<queue>
#include<vector>
using namespace std;
struct node{
  int v,dis;
  node(int _v,int _dis): v(_v),dis(_dis){}
}
const int maxn=1000;
const int inf=0x3ffffff;
int d[maxn]={};
int num[maxn]={}; //顶点入队次数
vector<node> adj[maxn];
bool inq[maxn]={false};

bool SPFA(int s){
  fill(d,d+maxn,inf);
  queue<int> q;
  q.push(s);
  inq[s]=true;
  num[s]++;
  d[s]=0;
  while(!q.empty()){
    int u=q.top();
    q.pop();
    inq[u]=false;
    for(int j=0;j<adj[u].size();j++){
      int v=adj[u][j].v;
      int dis=adj[u][j].dis;
      if(d[v]>d[u]+dis){
        d[v]=d[u]+dis;
        if(!inq[v]){
          q.push(v);
          inq[v]=true;
          num[v]++;
          if(num[v]>=n)
            return false;
        }
      }
    }
  }
  return true;
}

15.5.3.4. Floyd 全源最短路径

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
int dis[maxn][maxn]; //dis[i][j] i到j的最短距离
void Floyd(){
  for(int k=0;k<n;k++){
    for(int i=0;i<n;i++){
      for(int j=0;j<n;j++){
        if(dis[i][k]!=inf&&dis[k][j]!=inf
           &&dis[i][k]+dis[k][j]<dis[i][j]){
          dis[i][j]=dis[i][k]+dis[k][j];
        }
      }
    }
  }
}

int main(){
  fill(d[0],d[0]+maxn*maxn,inf);
  for(int i=0;i<n;i++){
    dis[i][i]=0;
  }
  scanf("%d%d",&u,&v);
  scanf("%d",&dis[u][v]);
}

15.5.4. 最小生成树

边数=顶点数-1，树内不会有环

满足整棵树的边权之和最小

15.5.4.1. prim

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=1000;
const int inf=0x03ffffff;
bool visit[maxn]={false};
int graph[maxn][maxn];
int d[maxn];
int ans=0;
int prim(int s){
  d[s]=0;
  for(int i=0;i<n;i++){
    int u=-1; int min=inf;
    for(int j=0;j<n;j++){
      if(visit[j]==false&&d[j]<min){
        min=d[j];
        u=j;
      }
    }
    if(u==-1){
      return;
    }
    visit[u]=true;
    ans+=d[u];
    for(int v=0;v<n;v++){
      if(visit[v]==false&&graph[u][v]!=inf){
        if(d[v]>graph[u][v]){
          d[v]=graph[u][v];
        }
      }
    }
  }
  return ans;
}

15.5.4.2. kruskal

点多，边少

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
struct node{
  int u,v,cost;
};
node edge[maxn];

bool cmp(node a,node b){
  return a.cost<b.cost;
}
int findfather(int x){
  int a=x;
  while(x!=father[x]){
    x=father[x];
  }
  while(a!=father[a]){
    int z=a;
    a=father[a];
    father[z]=x;
  }
  return x;
}
//n个顶点，m条边
int kruskal(int n,int m){
  int ans=0;
  int num=0; //总边数
  for(int i=1;i<=;i++){
    father[i]=i;
  }
  sort(edge,edge+m,cmp);
  for(int i=0;i<m;i++){
    int u=findfather(edge[i].u);
    int v=findfather(edge[i].v);
    if(u!=v){
      father[u]=v;
      ans+=edge[i].cost;
      num++;
      if(num==n-1)
        break;
    }
  }
  if(num1=n-1)
    return -1;
  else
    return ans;
}

15.5.5. 拓扑排序

图一定是有向无环图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
vector<int> G[maxn];
int n,m,inDegree[maxn];

bool topologicalSort(){
  int num=0;
  queue<int> q;
  for(int i=0;i<n;i++){
    if(inDegree[i]==0){
      q.push(i);
    }
  }
  while(!q.empty()){
    int u=q.front();
    q.pop();
    printf("%d",u);
    for(int i=0;i<G[u].size();i++){
      int v=G[u][i];
      inDegree[v]--;
      if(inDegree[v]==0){
        q.push(v);
      }
    }
    G[u].clear();
    num++;
  }
  if(num==n)
    return true;
  else
    return false;
}

15.5.6. 关键路径

ve[i] 事件i的最早发生时间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
vector<int> G[maxn];
int n,m,inDegree[maxn];
stack<int> s;

bool topologicalSort(){
  int num=0;
  queue<int> q;
  for(int i=0;i<n;i++){
    if(inDegree[i]==0){
      q.push(i);
    }
  }
  while(!q.empty()){
    int u=q.front();
    q.pop();
    s.push(u);
    for(int i=0;i<G[u].size();i++){
      int v=G[u][i].v;
      inDegree[v]--;
      if(inDegree[v]==0){
        q.push(v);
      }
    }
    G[u].clear();
    //ve[u]来更新所有后继结点v
    if(ve[u]+G[u][i].w>ve[v]){
      ve[v]=ve[u]+G[u][i].w;
    }
  }
  if(s.size()==n)
    return true;
  else
    return false;
}

vl[i] 事件i的最迟发生时间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
fill(vl,vl+n,ve[n-1]);

while(!s.empty()){
  int u=s.top();
  s.pop();
  
  for(int i=0;i<G[u].size();i++){
    int v=G[u][i].v;
    
    if(vl[v]-G[u][i].w<vl[u]){
      vl[u]=vl[v]-G[u][i].w;
    }
  }
  
}

关键路径

1
2
3
4
5
6
7
8
9
10
11
12
for(int u=0;u<n;u++){
  for(int i=0;i<G[u].size();i++){
    int v=G[u][i].v;
    int w=G[u][i].w;
    int e=ve[v];
    int l=vl[v]-w;
    if(e==l){
      printf("%d->%d",u,v); //关键路径
    }
  }
}
ve[n-1] //关键路径长度

16. 搜索

16.1. dfs 深度优先搜索

类似于递归，使用系统栈实现，存在岔路口(递归边界)和路(递归式)

16.1.1. 背包问题

n件物品，每件重量w[i]，价值c[i]，选出若干件物品放入容量为v的背包中，使得在选入背包的物品重量和不超过容量v的前提下，让背包中的物品的价值之和最大。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int maxValue=-1;
void dfs(int index,int sumW,int sumC){
  //死胡同
  if(index==n){
    return;
  }
  //不选
  dfs(index+1,sumW,sumC);
  //选
  if(sumW+w[index]<=v){
    if(sumC+c[index]>maxValue){
      maxValue=sumC+c[index];
    }
    dfs(index+1,sumW+w[index],sumC+c[index]);
  }
}

dfs(0,0,0);

16.2. bfs 广度优先搜索

队列实现

16.2.1. 迷宫步数

. . . . . .

. * . * .

. * S * .

. * * * .

. . . T *

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include<cstdio>
#include<queue>
using namespace std;
const int maxn=100;
struct node{
  int x,y;
  int step=0;
}S,T;

int n,m;
char matrix[maxn][maxn];
bool inq[maxn][maxn]={false};
int x[4]={0,0,1,-1};
int y[4]={1,-1,0,0};
bool judge(int x,int y){
  if(x>=n||x<0||y>=m||y<0)
    return false;
  if(matrix[x][y]=='*'||inq[x][y])
    return false;
  return true;
}
int bfs(){
  queuq<node> q;
  q.push(S);
  inq[S.x][S.y]=true;
  while(!q.empty()){
    node top=q.top();
    q.pop();
    if(top.x==T.x&&top.y==T.y){
      return top.step;
    }
    for(int i=0;i<4;i++){
      int nowX=top.x+x[i];
      int nowY=top.y+y[i];
      if(judge(nowX,nowY)){
        node newnode;
        newnode.x=nowX;
        newnode.y=nowY;
        newnode.step=top.step+1;
        q.push(newnode);
        inq[nowX][nowY]=true;
      }
    }
  }
  return -1;
}
int main(){
  scanf("%d%d",&n,&m);
  int ans=0;
  for(int i=0;i<n;i++){
    getchar();
    for(int j=0;j<m;j++){
      matrix[i][j]=getchar();
    }
    matrix[i][m+1]='\0';
  }
  scanf("%d%d%d%d",&S.x,&S.y,&T.x,&T.y);
  S.step=0;
  printf("%d\n",bfs());
  return 0;
}

17. 动态规划

17.1. 塔楼

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
//dp[i][j]表示从i行第j个数字出发的到达最底层的所有路径中能得到的最大和
//dp[i][j]=max(dp[i+1][j],dp[i+1][j+1])+f[i][j]

#include<stdio.h>
#include<algorithm>
using namespace std;
const int maxn=1000;
int dp[maxn][maxn],f[maxn][maxn];
int main(){
  int n;
  scanf("%d",&n);
  for(int i=1;i<=n;i++){
    for(int j=1;j<=i;j++){
      scanf("%d",&f[i][j]);
    }
  }
  
  //边界
  for(int j=1;j<=n;j++){
    dp[n][j]=f[n][j];
  }
  
  for(int i=n-1;i>=1;i--){
    for(int j=1;j<=i;j++){
      dp[i][j]=max(dp[i+1][j],dp[i+1][j+1])+f[i][j];
    }
  }
  
  printf("%d",dp[1][1]);
}

17.2. 最大连续子序列

A1，A2，A3，… ，An 序列，求i，j，使得Ai+ … +Aj 最大，输出这个最大和

dp[i]表示以a[i]作为末尾的连续序列的最大和

状态转移方程：dp[i]=max(a[i],dp[i-1]+a[i])

边界: dp[0]=a[0];

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
for(int i=0;i<n;i++){
  scanf("%d",&a[i]);
}

dp[0]=a[0];
for(int i=1;i<n;i++){
  dp[i]=max(a[i],dp[i-1]+a[i]);
}

int maxn=-1;
for(int i=0;i<n;i++){
  if(dp[i]<maxn){
    maxn=dp[i];
  }
}

17.3. 最长不下降子序列LIS

dp[i]表示以a[i]作为末尾的最长不下降子序列长度

dp[i]=max{1,dp[j]+1} (j=1,2,…,i-1) a[j]<a[i]

a[i]自成一派 or 跟到a[j]后

1
2
3
4
5
6
7
8
9
10
int ans=-1;
for(int i=1;i<=n;i++){
  dp[i]=1;
  for(int j=1;j<i;j++){
    if(a[i]>=a[j]&&(dp[j]+1>dp[i])){
      dp[i]=dp[j]+1;
    }
  }
  ans=max(ans,dp[i]);
}

17.4. 最长公共子序列LCS

dp[i] [j]表示字符串A的i号位和字符串B的j号位之前的LCS长度

dp[i] [j]=dp[i-1] [j-1]

$$dp[i][j]= \begin{cases} dp[i-1][j-1]+1& \text{a[i]==b[j]}\ max(dp[i-1][j],dp[i][j-1])& \text{a[i]!=b[j]} \end{cases}$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
for(int i=0;i<=lena;i++){
  dp[i][0]=0;
}
for(int i=0;i<=lenb;i++){
  dp[0][i]=0;
}

for(int i=1;i<=lena;i++){
  for(int j=1;j<=lenb;j++){
    if(a[i]==b[j]){
      dp[i][j]=dp[i-1][j-1]+1;
    }else{
      dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
    }
  }
}
return dp[lena][lenb];

17.5. 最长回文子串

dp[i] [j] 表示s[i]到s[j]所表示的子串是否为回文子串 1/0

$$dp[i][j]= \begin{cases} dp[i+1][j-1]& \text{s[i]==s[j]}\ 0& \text{s[i] !=s[j]} \end{cases}$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
int ans=1;
for(int i=0;i<len;i++){
  dp[i][i]=1;
  if(i<len-1){
    if(s[i]==s[i+1]){
      dp[i][i+1]=1;
      ans=2;
    }
  }
}

for(int L=3;L<=len;L++){
  for(int i=0;i+L-1<len;i++){
    int j=i+L-1;
    if(s[i]==s[j]&&dp[i+1][j-1]==1){
      dp[i][j]=1;
      ans=L;
    }
  }
}

return ans;

17.6. 背包问题

17.6.1. 01背包

dp[i] [v]前i件物品恰好装入容量为v的背包中所能获得的最大价值

  • 装第i件 计算前i-1件最大价值

  • 不装i件 计算前i-1件装v-w[i]所能获得的最大价值

dp[i] [v]=max(dp[i-1] [v],dp[i-1] [v-w[i]]+c[i])

边界 dp[0] [v]=0 (0<=v<=V)

最终 dp[n] [v] 中最大值

1
2
3
4
5
for(int i=1;i<=n;i++){
  for(int v=w[i];v<=V;v++){
    dp[i][v]=max(dp[i-1][v],dp[i-1][v-w[i]]+c[i]);
  }
}

简化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
for(int v=0;v<=V;v++){
  dp[v]=0;
}
for(int i=1;i<=n;i++){
  for(int v=V;v>=w[i];v--){
    dp[v]=max(dp[v],dp[v-w[i]]+c[i]);
  }
}

int max=-1;
for(int v=0;v<=V;v++){
  if(dp[v]>max){
    max=dp[v];
  }
}
return max;

17.6.2. 完全背包

放入i时，物品可以放任意件

dp[i] [v]=max(dp[i-1] [v],dp[i] [v-w[i]]+c[i])

1
2
3
4
5
for(int i=1;i<=n;i++){
  for(int v=w[i];v<=V;v++){
    dp[v]=max(dp[v],dp[v-w[i]]+c[i]);
  }
}

18. 字符串

18.1. hash

求n个字符串中不同字符串的个数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
const int MOD=1000000007; //1e9+7
const int P=10000019;

long long hashFunc(string str){
  long long H=0;
  for(int i=0;i<str.length();i++){
    H=(H*P+str[i]-'a')%MOD;
  }
}

int main(){
  string str;
  getline(cin,str);
  long long id=hashFunc(str);
  
  return 0;
}

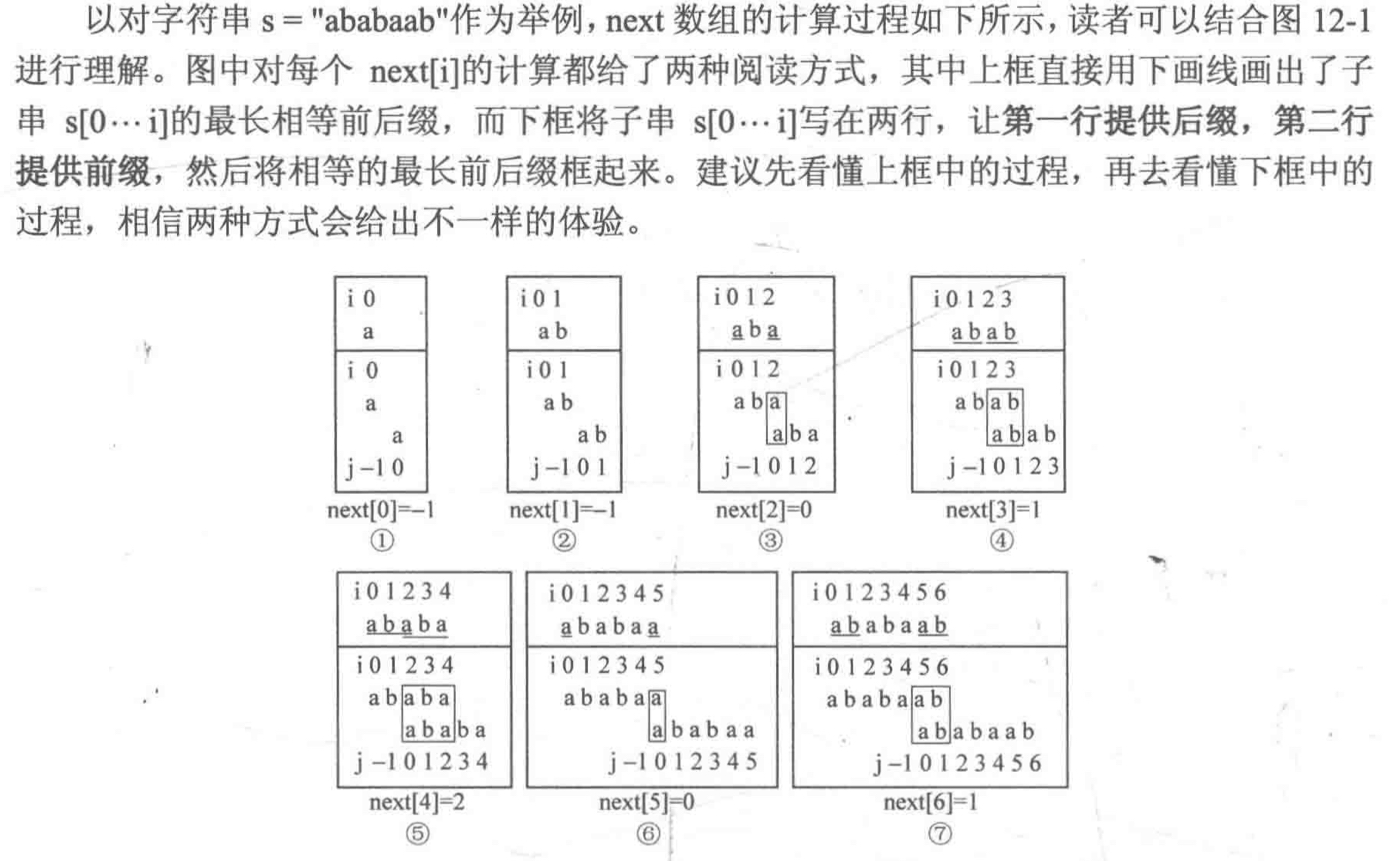
18.2. KMP

18.2.1. next[i]

所求最长相等前后缀中前缀最后一位的下标。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int next[maxn]={};
void getNext(char s[],int len){
  
    next[0]=-1;
    int j=-1;
    for(int i=1;i<len;i++){
      while(j!=-1&&s[i]!=s[j+1]){
        j=next[j];
      }
      if(s[i]==s[j+1]){
        j++;
      }
      next[i]=j;
    }
}

18.2.2. kmp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
bool KMP(char text[],char pattern[]){
  int n=strlen(text);
  int m=strlen(pattern);
  getNext(pattern,m);
  int j=-1;
  for(int i=0;i<n;i++){
    while(j!=-1&&text[i]!=pattern[j+1]){
      j=next[j];
    }
    if(text[i]==pattern[j+1]){
      j++;
    }
    if(j==m-1){
      return true;
    }
  }
  return false;
}

18.2.3. 统计模式串出现次数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int KMP(char text[],char pattern[]){
  int ans=0;
  int n=strlen(text);
  int m=strlen(pattern);
  getNext(pattern,m);
  int j=-1;
  for(int i=0;i<n;i++){
    while(j!=-1&&text[i]!=pattern[j+1]){
      j=next[j];
    }
    if(text[i]==pattern[j+1]){
      j++;
    }
    if(j==m-1){
      ans++;
      j=next[j];
    }
  }
  return ans;
}

18.2.4. 改进next[]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int nextval[maxn]={};
void getNext(char s[],int len){
  
    nextval[0]=-1;
    int j=-1;
    for(int i=1;i<len;i++){
      while(j!=-1&&s[i]!=s[j+1]){
        j=nextval[j];
      }
      if(s[i]==s[j+1]){
        j++;
      }
      if(j==-1||s[i]!=s[j+1]){
        nextval[i]=j;
      }
      else{
        nextval[j]=nextval[j];
      }
    }
}

19. 分块

table[100001] 分为317块，每块316个元素

block[i] 第i块中存在的元素个数

元素x所在块号 x/316：

block[x/316]++ 所在块元素个数+1

table[x]++ 元素x存在个数+1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
const int sqrN=316;
//添加元素
block[x/sqrN]++;
table[x]++;
//删除元素
block[x/sqrN]--;
table[x]--;
//第K大元素
int sum=0;
int id=0;
while(sum+block[id]<k){
  sum+=block[id++];
}
int num=id*sqrN;
while(sum+table[num]<k){
  sum+=table[num++];
}
return num;

20. 树状数组BIT

lowbit=x&(-x);

能整除x的最大2的幂次

c[i] 存放数组A中i号位之前lowbit(i)个元素之和

i 从1开始

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int getSum(int x){
  int sum=0;
  for(int i=x;i>0;i-=lowbit(i)){
    sum+=c[i];
  }
  return sum;
}


void update(int x,int v){
  for(int i=x;i<=N;i+=lowbit(i)){
    c[i]+=v;
  }
}

求序列中左边比该数小的数个数

1
2
3
4
5
6
7
8
9
int main(){
  int n,a;
  scanf("%d",&n);
  for(int i=0;i<n;i++){
    scanf("%d",&a);
    update(a,1);
  }
  getSum(x-1);
}
本文结束  感谢您的阅读
  • 本文作者： Wang Ting
  • 本文链接： /zh-CN/2019/11/13/算法笔记/
  • 发布时间： 2019-11-13 23:57
  • 更新时间： 2023-02-08 21:07
  • 版权声明： 本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！