A1130 Infix Expression (25 point(s))

树的中序遍历+根结点的查找

1. 原文

Given a syntax tree (binary), you are supposed to output the corresponding infix expression, with parentheses reflecting the precedences of the operators.

Input Specification:

Each input file contains one test case. For each case, the first line gives a positive integer N (≤ 20) which is the total number of nodes in the syntax tree. Then N lines follow, each gives the information of a node (the i-th line corresponds to the i-th node) in the format:

data left_child right_child

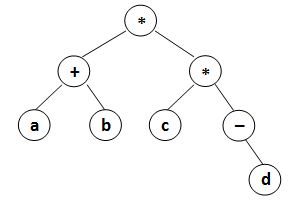
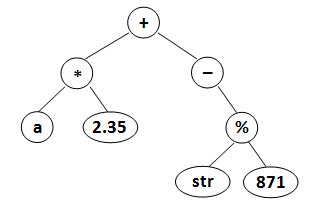
where data is a string of no more than 10 characters, left_child and right_child are the indices of this node’s left and right children, respectively. The nodes are indexed from 1 to N. The NULL link is represented by −1. The figures 1 and 2 correspond to the samples 1 and 2, respectively.

Figure 1	Figure 2

output Specification:

For each case, print in a line the infix expression, with parentheses reflecting the precedences of the operators. Note that there must be no extra parentheses for the final expression, as is shown by the samples. There must be no space between any symbols.

Sample Input 1:

8
* 8 7
a -1 -1
* 4 1
+ 2 5
b -1 -1
d -1 -1
- -1 6
c -1 -1

Sample output 1:

(a+b)*(c*(-d))

Sample Input 2:

8
2.35 -1 -1
* 6 1
- -1 4
% 7 8
+ 2 3
a -1 -1
str -1 -1
871 -1 -1

Sample Output 2:

(a*2.35)+(-(str%871))

2. 解析

结点在1-N之间，只给了结点值，结点左右指向。

• 得到根结点 indegree[i]==0

​ 记录左右结点 indegree[a]++； indegree[b]++；

• 遍历

  中序遍历 左根右

  tree[idx].data=experssion(tree[idx].lchild)+tree[idx].data+experssion(tree[idx].rchild);

3. AC代码

#include<cstdio>
#include<string>
using namespace std;
struct node{
	string data;
	int lchild,rchild;
}tree[30];
int indegree[30]={};
int root=0;
string experssion(int idx){
	if (idx==-1)
	{
		return "";
	}
	if (tree[idx].rchild!=-1)
	{
		tree[idx].data=experssion(tree[idx].lchild)+tree[idx].data+experssion(tree[idx].rchild);
	    if (idx!=root)
	    {
	    	tree[idx].data="("+tree[idx].data+")";
	    }
	}
	return tree[idx].data;
}
char str[30];
int main()
{
	int n;
	scanf("%d",&n);
	for (int i = 1; i <= n; ++i)
	{
		scanf("%s%d%d",str,&tree[i].lchild,&tree[i].rchild);
		tree[i].data=str;
		indegree[tree[i].lchild]++;
		indegree[tree[i].rchild]++;
	}
	for (int i = 1; i <= n; ++i)
	{
		if (indegree[i]==0)
		{
			root=i;
			break;
		}
	}
	string ans=experssion(root);
	printf("%s\n", ans.c_str());
	return 0;
}